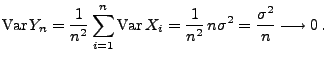Theorem 5.13
Sei
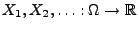
eine Folge von Zufallsvariablen mit dem
gleichen Erwartungswert
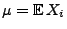
und
mit
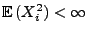
für alle
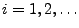
.
- 1.
- Falls
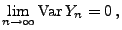 |
(16) |
dann gilt
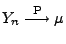 .
.
- 2.
- Die Bedingung
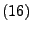 ist insbesondere
dann erfüllt, wenn die Zufallsvariablen
ist insbesondere
dann erfüllt, wenn die Zufallsvariablen
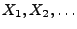 unabhängig sind mit der gleichen
Varianz
unabhängig sind mit der gleichen
Varianz
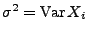 für alle
für alle
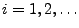 .
.