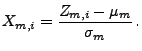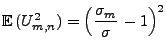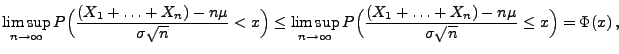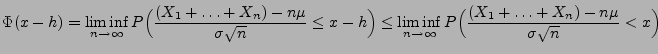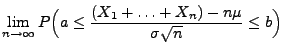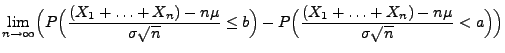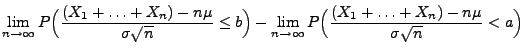Next: Anwendungsbeispiele
Up: Zentraler Grenzwertsatz
Previous: Zentraler Grenzwertsatz
Contents
Zentraler Grenzwertsatz für Summen von
unabhängigen Zufallsvariablen
In Verallgemeinerung des zentralen Grenzwertsatzes von
DeMoivre-Laplace, der bereits in Abschnitt 3.2.4 erwähnt
wurde, leiten wir den folgenden zentralen Grenzwertsatz für Summen
von unabhängigen und identisch verteilten Zufallsvariablen her.
Theorem 5.16
Sei
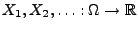
eine Folge von unabhängigen und identisch verteilten
Zufallsvariablen mit
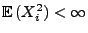
und
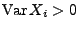
für alle
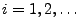
;
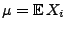
,
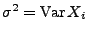
. Dann gilt für jedes
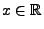
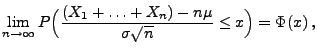 |
(44) |
wobei
![$ \Phi:\mathbb{R}\to[0,1]$](img2046.png)
die Verteilungsfunktion der
Standardnormalverteilung ist.
Im Beweis von Theorem 5.16 benutzen wir eine
Approximationsmethode, die auf G. Kersting zurückgeht. Dabei
benötigen wir mehrere Hilfssätze, die auch von eigenständigem
Interesse sind.
Zunächst betrachten wir eine Reihe von analytischen Eigenschaften
der Verteilungsfunktion 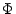 der N
der N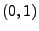 -Verteilung, die
gegeben ist durch
-Verteilung, die
gegeben ist durch
Lemma 5.6
- 1.
- Die Funktion
![$ \Phi:\mathbb{R}\to[0,1]$](img2046.png) ist unendlich oft differenzierbar.
ist unendlich oft differenzierbar.
- 2.
- Sämtliche Ableitungen
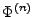 von
von 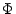 sind beschränkte
Funktionen
sind beschränkte
Funktionen
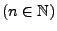 , und es gilt
, und es gilt
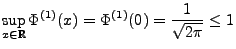 |
(45) |
und
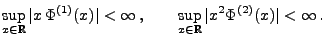 |
(46) |
- 3.
- Außerdem gilt die Identität
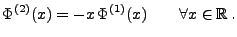 |
(47) |
Der Beweis von Lemma 5.6 wird in den Übungen
behandelt; vgl. Übungsaufgabe 13.1.
Der nächste Hilfssatz enthält eine nützliche (gleichmäßige)
Stetigkeitseigenschaft von 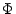 .
.
Lemma 5.7
Sei
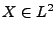
eine beliebige Zufallsvariable mit
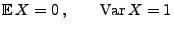 |
(48) |
und
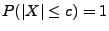 |
(49) |
für eine Konstante
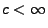
. Mit der Schreibweise
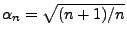
und
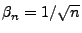
gilt dann für
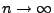
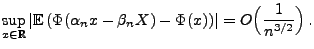 |
(50) |
- Beweis
-
- Für
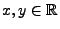 mit
mit 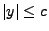 entwickeln wir die
Verteilungsfunktion
entwickeln wir die
Verteilungsfunktion 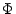 im Punkt
im Punkt
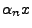 in eine
Taylor-Reihe und erhalten
in eine
Taylor-Reihe und erhalten
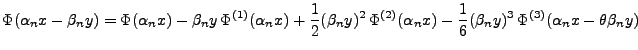 |
(51) |
mit
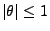 .
.
- Weil
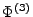 beschränkt ist und
beschränkt ist und 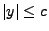 , hat der letzte
Summand auf der rechten Seite von (51) die
Größenordnung
, hat der letzte
Summand auf der rechten Seite von (51) die
Größenordnung
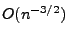 .
.
- Durch Taylorentwicklung der Funktion
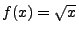 im Punkt
im Punkt
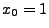 ergibt sich, dass
ergibt sich, dass
- Deshalb ergibt die Taylorentwicklung von
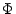 im Punkt
im Punkt 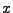 den
Ausdruck
den
Ausdruck
mit
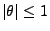 .
.
- Wegen (46) ergibt sich hieraus, dass
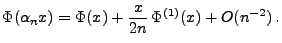 |
(52) |
- Auf ähnliche Weise ergibt sich, dass
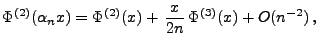 |
(53) |
wobei
- Wenn nun (52) und (53) in die
Taylor-Reihe (51) eingesetzt werden, ergibt sich
der Ausdruck
- Weil
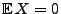 und
und
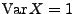 vorausgesetzt wird (vgl.
(48)), folgt hieraus, dass
vorausgesetzt wird (vgl.
(48)), folgt hieraus, dass
- Wegen der Identität
für jedes
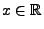 (vgl. (47)), ergibt dies die
Behauptung.
(vgl. (47)), ergibt dies die
Behauptung.

- Definition
 Für beliebige Verteilungsfunktionen
Für beliebige Verteilungsfunktionen
![$ F,G:\mathbb{R}\to[0,1]$](img2079.png) sei
sei
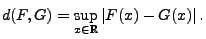 |
(54) |
Die in (54) gegebene Abstandsfunktion heißt Supremum-Metrik.
- Beachte
 Anstelle
Anstelle 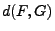 schreiben wir manchmal auch
schreiben wir manchmal auch 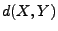 oder
oder 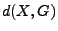 , falls
, falls  und
und 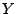 Zufallsvariablen mit den
Verteilungsfunktionen
Zufallsvariablen mit den
Verteilungsfunktionen 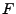 bzw.
bzw. 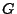 sind.
sind.
Lemma 5.8
Seien
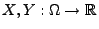
beliebige Zufallsvariablen mit
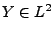
, und sei
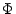
die Verteilungsfunktion der
Standardnormalverteilung N
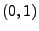
. Falls
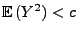
, dann gilt
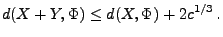 |
(55) |
- Beweis
-
- Für die erste Ableitung
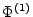 von
von 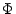 gilt
gilt
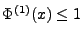 für jedes
für jedes
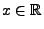 ; vgl.
(45).
; vgl.
(45).
- Hieraus folgt, dass für beliebige
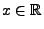 und
und 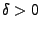
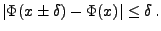 |
(56) |
- Außerdem gilt
und
- Also gilt
- Wegen (56) ergibt sich nun hieraus, dass
- Wenn die erste Ungleichung mit
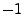 multipliziert wird, dann
impliziert dies, dass
und
multipliziert wird, dann
impliziert dies, dass
und
- Hieraus folgt, dass
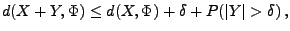 |
(57) |
weil
- Genauso wie im Beweis der Tschebyschew-Ungleichung
(4.72) kann man zeigen, dass für jedes
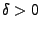
- Für
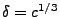 ergibt sich hieraus und aus
ergibt sich hieraus und aus
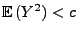 ,
dass
,
dass
- Dies und (57) liefert nun die Behauptung.

In dem folgenden Hilfssatz leiten wir Bedingungen her, unter denen
die Summe von unabhängigen (nichtnotwendig identisch verteilten)
diskreten Zufallsvariablen näherungsweise normalverteilt ist.
Lemma 5.9
Seien
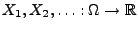
unabhängige diskrete
Zufallsvariable, die jeweils nur endlich viele verschiedene Werte
mit positiver Wahrscheinlichkeit annehmen. Falls
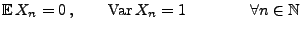 |
(58) |
und falls es eine Konstante
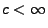
gibt, so dass
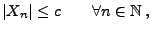 |
(59) |
dann gilt
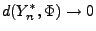 |
(60) |
für
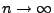
, wobei
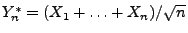
.
- Beweis
-
- Sei
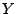 eine N
eine N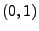 -verteilte Zufallsvariable, die unabhängig
von der Folge
-verteilte Zufallsvariable, die unabhängig
von der Folge
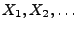 ist.
ist.
- Für eine beliebige, jedoch fest vorgegebene natürliche Zahl
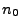 und für jedes
und für jedes 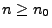 betrachten wir die Zufallsvariable
wobei
betrachten wir die Zufallsvariable
wobei
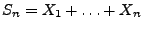 .
.
- Dann gilt
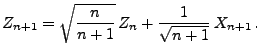 |
(61) |
- Die Zufallsvariable
 möge die Werte
möge die Werte
 mit
den Wahrscheinlichkeiten
mit
den Wahrscheinlichkeiten
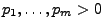 annehmen;
annehmen;
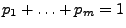 .
.
- Weil die beiden Summanden auf der rechten Seite von
(61) unabhängig sind, lässt sich die
Verteilungsfunktion
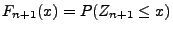 von
von 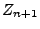 wie
folgt durch
wie
folgt durch
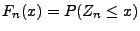 ausdrücken:
ausdrücken:
- Mit der Schreibweise
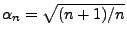 und
und
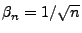 ergibt sich hieraus, dass
ergibt sich hieraus, dass
- Also gilt
weil
- Wegen Lemma 5.7 gibt es deshalb eine Konstante
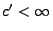 , so dass für jedes
, so dass für jedes
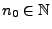 und für jedes
und für jedes
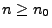
- Weil
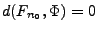 , ergibt sich hieraus, dass
, ergibt sich hieraus, dass
- Weil die Reihe in der letzten Abschätzung gegen einen endlichen
Grenzwert konvergiert, gibt es für jedes
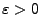 ein
ein
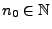 , so dass für jedes
, so dass für jedes 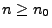
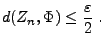 |
(62) |
- Außerdem ergibt sich aus der Rekursionsformel (61),
dass für jedes
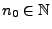 und dass somit
und dass somit
- Hieraus und aus (62) ergibt sich wegen
Lemma 5.8, dass für jedes hinreichend große

- Weil
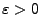 beliebig klein gewählt werden kann, ist damit
die Behauptung bewiesen.
beliebig klein gewählt werden kann, ist damit
die Behauptung bewiesen.

- Beweis von Theorem 5.16
-
- Für jedes
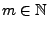 setzen wir
setzen wir
- Außerdem sei
- Dann gilt für
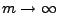
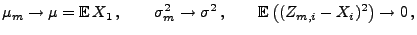 |
(63) |
vgl. Übungsaufgabe 14.2.
- Für beliebige
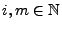 betrachten wir nun die Zufallsvariable
betrachten wir nun die Zufallsvariable
- Weil dann die Folge
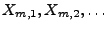 den Bedingungen von
Lemma 5.9 für jedes beliebige, jedoch fest
vorgegebene
den Bedingungen von
Lemma 5.9 für jedes beliebige, jedoch fest
vorgegebene
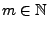 genügt, gilt also
genügt, gilt also
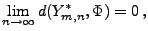 |
(64) |
wobei
- Wir betrachten nun die Differenz
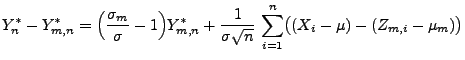 |
(65) |
und schätzen ihr zweites Moment nach oben ab, wobei
- Wenn wir die beiden Summanden auf der rechten Seite der Identität
(65) mit
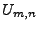 bzw.
bzw. 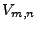 bezeichnen,
dann erhalten wir
und
weil die Summanden von
bezeichnen,
dann erhalten wir
und
weil die Summanden von 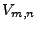 unabhängig und identisch verteilt
sind und weil ihr Erwartungswert gleich Null ist.
unabhängig und identisch verteilt
sind und weil ihr Erwartungswert gleich Null ist.
- Aus (63) und aus der Minkowski-Ungleichung
(4.68) ergibt sich nun, dass
- Hieraus und aus (64) ergibt sich mit Hilfe von
Lemma 5.8, dass

Korollar 5.4
Unter den Voraussetzungen von Theorem
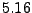
gilt
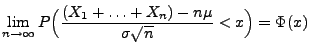 |
(66) |
für jedes
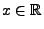
, und
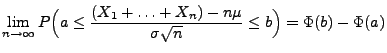 |
(67) |
für beliebige
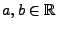
mit
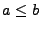
.
- Beweis
-
- Die Behauptung (66) ergibt sich
aus Theorem 5.16, weil
weil für jedes
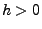 und weil die Verteilungsfunktion
und weil die Verteilungsfunktion 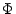 der
N
der
N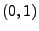 -Verteilung stetig ist.
-Verteilung stetig ist.
- Die Behauptung (67) ergibt sich nun
aus Theorem 5.16 und aus (66), denn es gilt





Next: Anwendungsbeispiele
Up: Zentraler Grenzwertsatz
Previous: Zentraler Grenzwertsatz
Contents
Ursa Pantle
2004-05-10
![]() der N
der N![]() -Verteilung, die
gegeben ist durch
-Verteilung, die
gegeben ist durch
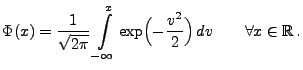
![]() .
.
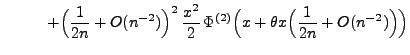
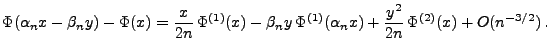
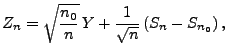
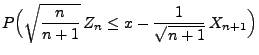
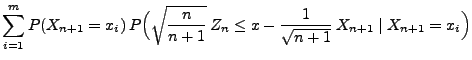
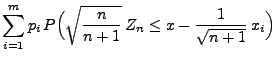
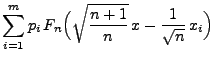
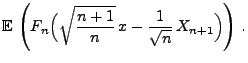
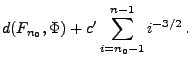
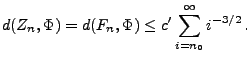
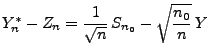
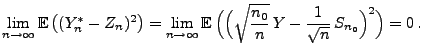
![$\displaystyle \varphi_m(x)=\left\{\begin{array}{ll} \displaystyle\frac{k}{m}\;,...
...{m}$\ mit $-m^2\le k\le m^2$,}\\ [3\jot]
0 & \mbox{sonst.}
\end{array}\right.
$](img2141.png)