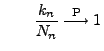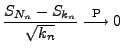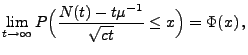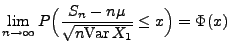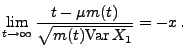- Seien
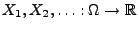 unabhängige und identisch
verteilte Zufallsvariablen mit
unabhängige und identisch
verteilte Zufallsvariablen mit
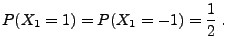
- Wir deuten
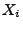 als den zufälligen Gewinn beim
als den zufälligen Gewinn beim 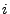 -ten Münzwurf
und betrachten die maximale (kumulative) Gewinnsumme
die beim
-ten Münzwurf
und betrachten die maximale (kumulative) Gewinnsumme
die beim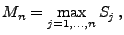
 -maligen Werfen einer Münze erzielt wird, wobei
-maligen Werfen einer Münze erzielt wird, wobei
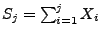 .
.
- Es gilt
- D.h., die normierten Maxima
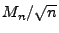 streben in Verteilung
gegen die sogenannte asymmetrische (Standard-)
Normalverteilung.
streben in Verteilung
gegen die sogenannte asymmetrische (Standard-)
Normalverteilung.
- Dies kann man sich wie folgt überlegen: Für jedes
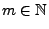 gilt
gilt
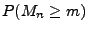
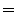
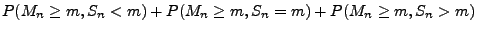
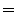
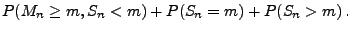
- Außerdem gilt
denn
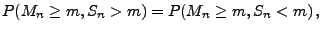
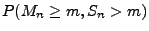
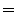
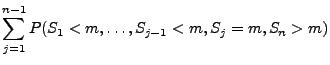
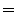
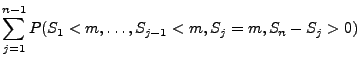
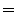
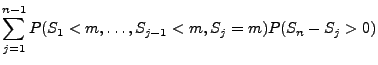
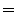
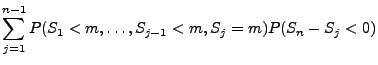
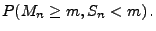
- Also gilt für jedes
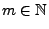
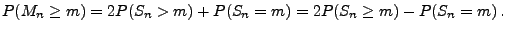
- Hieraus folgt, dass für jedes
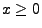 und
und
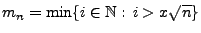
- Weil
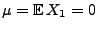 und
und
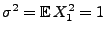 , ergibt sich aus
Theorem 5.16, dass
und dass es für jedes
, ergibt sich aus
Theorem 5.16, dass
und dass es für jedes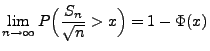
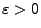 ein
ein
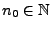 gibt, so
dass
für jedes
gibt, so
dass
für jedes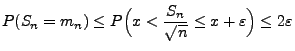
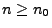 , wobei sich die letzte Ungleichung aus
(45) und durch die erneute Anwendung von
Theorem 5.16 ergibt.
, wobei sich die letzte Ungleichung aus
(45) und durch die erneute Anwendung von
Theorem 5.16 ergibt.
- Hieraus und aus (69) ergibt sich nun die Behauptung (68).
- So wie in dem Beispiel, das bereits in
Abschnitt 4.4.3 betrachtet wurde, nehmen wir
an, dass die
 -te Messung einer (unbekannten) Größe
-te Messung einer (unbekannten) Größe
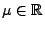 den Wert
den Wert
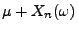 liefert für
liefert für
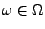 .
.
- Die Messfehler
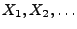 seien unabhängige und
identisch verteilte Zufallsvariablen.
seien unabhängige und
identisch verteilte Zufallsvariablen.
- Über die Verteilung von
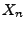 sei lediglich bekannt,
dass
sei lediglich bekannt,
dass
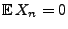 und
und
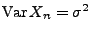 .
.
- Ein Ansatz zur ,,Schätzung'' der unbekannten Größe
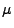 ist durch das arithmetische Mittel
der zufälligen Messwerte
ist durch das arithmetische Mittel
der zufälligen Messwerte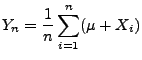
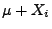 gegeben.
gegeben.
- Mit Hilfe von Korollar 5.4
lässt sich die
Wahrscheinlichkeit
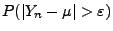 , dass der
Schätzfehler
, dass der
Schätzfehler 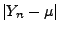 größer als
größer als
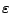 ist,
näherungsweise bestimmen.
ist,
näherungsweise bestimmen.
- Und zwar gilt für große


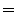
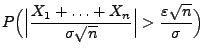
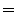
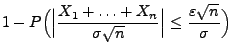
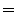
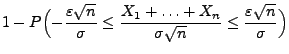
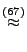
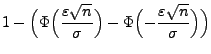
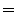
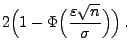
- Mit Hilfe des Satzes von Slutsky (vgl. die Theoreme 5.9 und 5.11) zeigen wir nun, wie die Aussage von Theorem 5.16 auf den Fall von Summen mit einer zufälligen Anzahl von Summanden übertragen werden kann.
- Seien
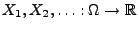 unabhängige und identisch
verteilte Zufallsvariablen mit
unabhängige und identisch
verteilte Zufallsvariablen mit
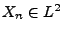 und
und
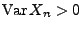 .
.
- Ohne Einschränkung der Allgemeinheit setzen wir voraus, dass
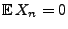 und
und
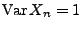 .
.
- Außerdem sei
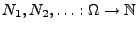 eine Folge von
Zufallsvariablen, so dass
eine Folge von
Zufallsvariablen, so dass
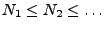 und
und
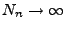 mit Wahrscheinlichkeit 1.
mit Wahrscheinlichkeit 1.
- Falls es Konstanten
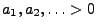 und
und 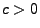 mit
mit
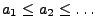 und
und
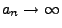 gibt, so dass
gibt, so dass
für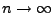 , dann gilt
, dann gilt
wobei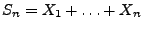 und
und 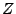 eine N
eine N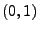 -verteilte
Zufallsvariable ist.
-verteilte
Zufallsvariable ist.
- Die Gültigkeit von (71) kann man sich wie folgt überlegen.
- Sei
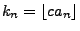 der ganzzahlige Anteil von
der ganzzahlige Anteil von
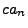 .
.
- Wegen (70) gilt dann auch
für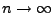 .
.
- Außerdem gilt
und, wegen Theorem 5.16,
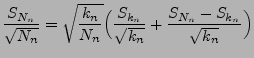
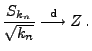
- Wegen (72) und wegen des Satzes von Slutsky
(vgl. die Theoreme 5.9 und 5.11) genügt
es nun noch zu zeigen, dass
für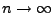 .
.
- Für beliebige
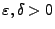 gilt
gilt
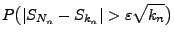
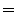
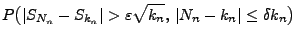
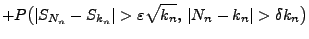
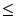
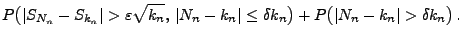
- Wegen (72) konvergiert der zweite Summand gegen
0 für
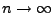 .
.
- Der erste Summand lässt sich wie folgt weiter nach oben
abschätzen:
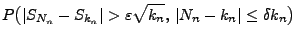
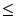
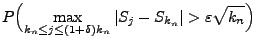
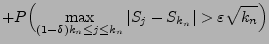
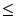
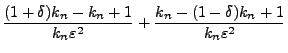
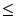
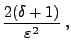
wobei sich die vorletzte Abschätzung aus der Ungleichung von Kolmogorow (vgl. Lemma 5.2) ergibt. - Weil
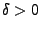 beliebig klein gewählt werden kann, ergibt sich
hieraus die Gültigkeit von (73).
beliebig klein gewählt werden kann, ergibt sich
hieraus die Gültigkeit von (73).
- Damit ist die erste Teilaussage in (71) bewiesen. Die zweite Teilaussage ergibt sich aus der ersten Teilaussage in (71) und aus dem Satz von Slutsky (vgl. die Theorem 5.11).
- Seien
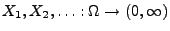 unabhängige und
identisch verteilte Zufallsvariable, die nur positive Werte
annehmen können;
unabhängige und
identisch verteilte Zufallsvariable, die nur positive Werte
annehmen können;
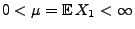 ,
,
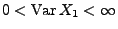 .
.
- Dann kann man
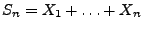 als den
als den  -ten Erneuerungszeitpunkt eines (biologischen, ökonomischen,
technischen) Systems auffassen; vgl. Beispiel 6 in
Abschnitt 5.2.3.
-ten Erneuerungszeitpunkt eines (biologischen, ökonomischen,
technischen) Systems auffassen; vgl. Beispiel 6 in
Abschnitt 5.2.3.
- Wir betrachten die zufällige Anzahl
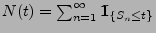 von Erneuerungen im Intervall
von Erneuerungen im Intervall ![$ (0,t]$](img2017.png) ;
;
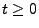 .
.
- Für den Erneuerungszählprozess
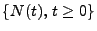 kann man nun
den folgenden zentralen Grenzwertsatz beweisen.
kann man nun
den folgenden zentralen Grenzwertsatz beweisen.
- Für jedes
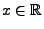 gilt
gilt
wobei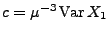 und
und 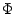 die Verteilungsfunktion
der Standardnormalverteilung ist.
die Verteilungsfunktion
der Standardnormalverteilung ist.
- Die Gültigkeit von (74) ergibt sich aus den folgenden Überlegungen.
- Zunächst ergibt sich unmittelbar aus dem Beweis von
Theorem 5.16, dass die Konvergenz
gleichmäßig in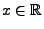 erfolgt.
erfolgt.
- Mit der Schreibweise
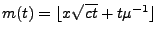 gilt außerdem
gilt außerdem
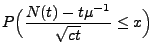
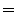
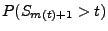
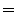
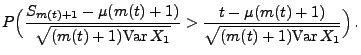
- Also gilt
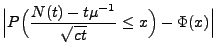
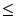
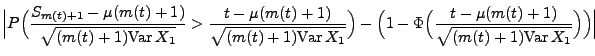
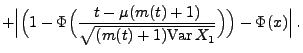
- Außerdem gilt für jedes
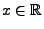
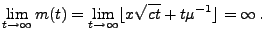
- Wegen (75) und wegen der Symmetrieeigenschaft
der Verteilungsfunktion
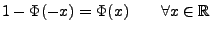
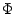 der N
der N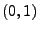 -Verteilung genügt es
somit noch zu zeigen, dass
-Verteilung genügt es
somit noch zu zeigen, dass
- Weil
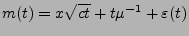 mit
mit
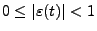 für jedes
für jedes 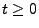 gilt
gilt
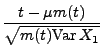
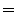
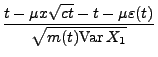
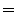
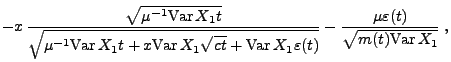
wobei der erste Summand gegen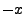 und der zweite Summand gegen 0
strebt für
und der zweite Summand gegen 0
strebt für
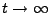 .
.
- Damit ist die Behauptung (74) bewiesen.
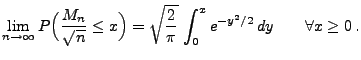
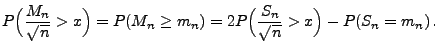
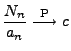
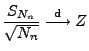 und
und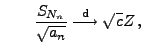
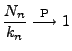 bzw.
bzw.