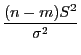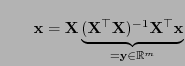Nächste Seite: Tests für die Regressionskoeffizienten;
Aufwärts: Normalverteilte Störgrößen
Vorherige Seite: Maximum-Likelihood-Schätzer
Inhalt
Verteilungs- und Unabhängigkeitseigenschaften
von
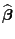 und
und 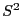
- Außer der bereits in (27) erwähnten
Normalverteilungseigenschaft
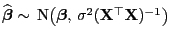 lässt
sich auch die Verteilung des Schätzers
lässt
sich auch die Verteilung des Schätzers
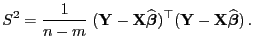 |
(37) |
für die Varianz 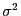 der Störgrößen bestimmen.
der Störgrößen bestimmen.
- Hierfür benutzen wir die Darstellungsformel
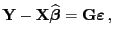 |
(38) |
die wir im Beweis von Theorem 2.5 gezeigt hatten,
wobei
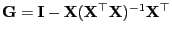 .
.
Dabei benötigen wir die folgende Rangformel, die wir hier
ohne Beweis angeben; vgl. Theorem 2.2.2 im Skript zur Vorlesung ,,
Lineare Algebra'' von W. Lütkebohmert (Universität Ulm,
Wintersemester 2005/06).
Lemma 2.3

Sei

eine beliebige
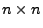
Matrix. Dann gilt
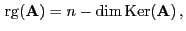 |
(39) |
wobei
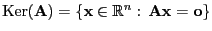
und
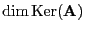
die Dimension von
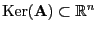
bezeichnet.
Aus der in Theorem 1.9 hergeleiteten Bedingung für
die  -Verteiltheit von quadratischen Formen
normalverteilter Zufallsvektoren ergibt sich nun das folgende
Resultat.
-Verteiltheit von quadratischen Formen
normalverteilter Zufallsvektoren ergibt sich nun das folgende
Resultat.
Theorem 2.7

Es gilt
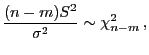 |
(40) |
d.h., die Zufallsvariable
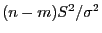
hat eine (zentrale)

-Verteilung mit
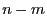
Freiheitsgraden.
- Beweis
-
Außerdem nutzen wir das in Theorem 1.10 hergeleitete
Kriterium für die Unabhängigkeit von linearen bzw. quadratischen
Formen normalverteilter Zufallsvektoren, um das folgende
Resultat zu zeigen.
- Beweis
-
- Aus
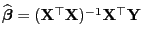 und
und
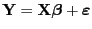 ergibt sich, dass
ergibt sich, dass
- Außerdem hatten wir im Beweis von Theorem 2.7
gezeigt, dass sich der Schätzer
als quadratische Form von
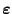 darstellen lässt:
darstellen lässt:
- Weil
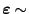 N
N
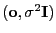 und weil
ergibt sich aus Theorem 1.10, dass die lineare Form
und weil
ergibt sich aus Theorem 1.10, dass die lineare Form
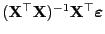 und die quadratische
Form
und die quadratische
Form
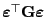 unabhängig sind.
unabhängig sind.
- Damit sind auch die Zufallsvariablen
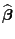 und
und 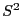 unabhängig.
unabhängig.





Nächste Seite: Tests für die Regressionskoeffizienten;
Aufwärts: Normalverteilte Störgrößen
Vorherige Seite: Maximum-Likelihood-Schätzer
Inhalt
Hendrik Schmidt
2006-02-27
![]() -Verteiltheit von quadratischen Formen
normalverteilter Zufallsvektoren ergibt sich nun das folgende
Resultat.
-Verteiltheit von quadratischen Formen
normalverteilter Zufallsvektoren ergibt sich nun das folgende
Resultat.