Next: Beispiele: Zufallsvektoren mit unabhängigen
Up: Zufallsvektoren
Previous: Bedingte Wahrscheinlichkeitsfunktion; bedingte Verteilung;
Contents
Unabhängige Zufallsvariablen
Die Unabhängigkeit von Zufallsvariablen wird durch den in
Abschnitt 2.7 eingeführten Begriff der Unabhängigkeit
von Ereignissen ausgedrückt.
So heißen zwei Zufallsvariablen
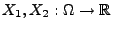 unabhängig,
wenn die Ereignisse
unabhängig,
wenn die Ereignisse
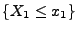 und
und
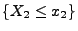 für
beliebige
für
beliebige
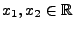 unabhängig sind.
unabhängig sind.
Für Folgen von Zufallsvariablen wird der Begriff der
Unabhängigkeit folgendermaßen gebildet.
- Definition
 Sei
Sei
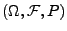 ein beliebiger
Wahrscheinlichkeitsraum.
ein beliebiger
Wahrscheinlichkeitsraum.
- Die Zufallsvariablen
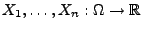 heißen unabhängig, falls
heißen unabhängig, falls
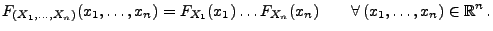 |
(26) |
- Sei
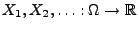 eine beliebige (unendliche) Folge
von Zufallsvariablen. Dann sagt man, dass
eine beliebige (unendliche) Folge
von Zufallsvariablen. Dann sagt man, dass
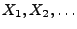 unabhängige Zufallsvariablen
sind, falls jede endliche Teilfolge
unabhängige Zufallsvariablen
sind, falls jede endliche Teilfolge
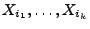 von
von
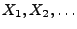 aus unabhängigen Zufallsvariablen besteht.
aus unabhängigen Zufallsvariablen besteht.
- Beachte
-
- Aus den Definitionen der
Verteilungsfunktionen
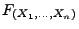 und
und
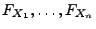 ergibt sich sofort, dass die
Definitionsgleichung (26) äquivalent ist mit
ergibt sich sofort, dass die
Definitionsgleichung (26) äquivalent ist mit
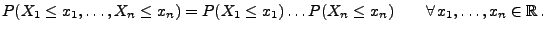 |
(27) |
- Darüber hinaus kann man zeigen, dass (27) und damit auch
(26) äquivalent ist mit der folgenden
(scheinbar schärferen) Bedingung.
Theorem 3.10
Die Zufallsvariablen
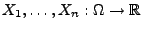
sind genau dann
unabhängig, wenn
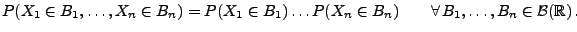 |
(28) |
- Beweis
-
- Es ist klar, dass (27) aus (28) folgt.
Hierfür genügt es,
![$ B_i=(-\infty,x_i]$](img834.png) zu setzen.
zu setzen.
- Umgekehrt ergibt sich (28) aus (27) aus
dem Monotone Class Theorem (vgl.Theorem 3.2), wobei
ähnlich wie im Beweis von Theorem 3.4 vorgegangen
werden kann.

Hieraus und aus den Definitionsgleichungen (12) und
(23) von
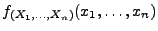 und
und
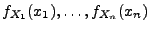 ergibt sich unmittelbar die
folgende Charakterisierung der Unabhängigkeit von diskreten bzw.
absolutstetigen Zufallsvariablen.
ergibt sich unmittelbar die
folgende Charakterisierung der Unabhängigkeit von diskreten bzw.
absolutstetigen Zufallsvariablen.
- Beweis





Next: Beispiele: Zufallsvektoren mit unabhängigen
Up: Zufallsvektoren
Previous: Bedingte Wahrscheinlichkeitsfunktion; bedingte Verteilung;
Contents
Ursa Pantle
2004-05-10
![]() unabhängig,
wenn die Ereignisse
unabhängig,
wenn die Ereignisse
![]() und
und
![]() für
beliebige
für
beliebige
![]() unabhängig sind.
unabhängig sind.
![]() und
und
![]() ergibt sich unmittelbar die
folgende Charakterisierung der Unabhängigkeit von diskreten bzw.
absolutstetigen Zufallsvariablen.
ergibt sich unmittelbar die
folgende Charakterisierung der Unabhängigkeit von diskreten bzw.
absolutstetigen Zufallsvariablen.