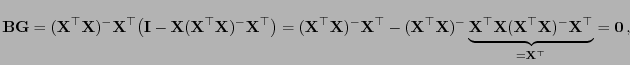Nächste Seite: Tests linearer Hypothesen
Aufwärts: Normalverteilte Störgrößen
Vorherige Seite: Normalverteilte Störgrößen
Inhalt
Maximum-Likelihood-Schätzer
- Genauso wie im Fall von Designmatrizen mit vollem Spaltenrang, der
in Abschnitt 2.2.1 diskutiert wurde, ergibt sich
aus Theorem 1.3, dass der Vektor
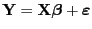 der Zielvariablen normalverteilt ist
mit
der Zielvariablen normalverteilt ist
mit
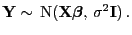 |
(56) |
- Mit anderen Worten: Der Zufallsvektor
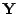 ist absolutstetig
mit der Dichte
ist absolutstetig
mit der Dichte
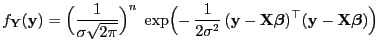 |
(57) |
für jedes
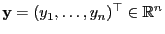 .
.
- Die Loglikelihood-Funktion
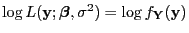 hat somit die Gestalt
hat somit die Gestalt
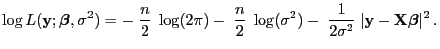 |
(58) |
- Um einen Maximum-Likelihood-Schätzer für den Parametervektor
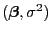 zu bestimmen, betrachten wir zunächst
(genauso wie im Beweis von Theorem 2.6) für
beliebige, jedoch fest vorgegebene
zu bestimmen, betrachten wir zunächst
(genauso wie im Beweis von Theorem 2.6) für
beliebige, jedoch fest vorgegebene
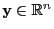 und
und
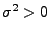 die Abbildung
die Abbildung
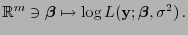 |
(59) |
- Aus (58) und (59) ergibt sich, dass
dabei der folgende Ausdruck
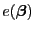 minimiert werden muss,
wobei
minimiert werden muss,
wobei
- Aus Theorem 3.6 folgt somit, dass der KQ-Schätzer
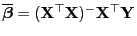 gleichzeitig ein ML-Schätzer für
gleichzeitig ein ML-Schätzer für
 ist (der nicht von
ist (der nicht von
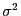 abhängt).
abhängt).
- Außerdem ergibt sich genauso wie im Beweis von
Theorem 2.6, dass durch
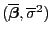 ein ML-Schätzer für
ein ML-Schätzer für
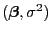 gegeben ist, wobei
gegeben ist, wobei
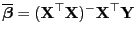 und und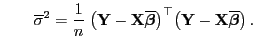 |
(60) |
- Beachte
-
- Beweis
-
- Aus Lemma 3.5 ergibt sich, dass
- In Lemma 3.5 hatten wir gezeigt, dass
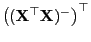 eine verallgemeinerte
Inverse von
eine verallgemeinerte
Inverse von
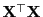 ist. Somit ergibt sich aus
Lemma 3.7, dass
ist. Somit ergibt sich aus
Lemma 3.7, dass
- Damit ist die erste Teilaussage bewiesen. Um die zweite
Teilaussage zu beweisen, genügt es zu beachten, dass
wobei sich die vorletzte Gleichheit aus Lemma 3.6
ergibt.
- Die dritte Teilaussage lässt sich wie folgt zeigen:
- Aus Lemma 3.2 und aus Lemma 3.6 ergibt
sich, dass
d.h.,
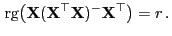 |
(62) |
- Aus Lemma 3.5 ergibt sich, dass die Matrix
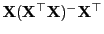 idempotent ist, denn es gilt
idempotent ist, denn es gilt
- Weil
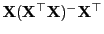 außerdem symmetrisch
ist, folgt aus Lemma 1.3 mit Hilfe von
(62), dass
außerdem symmetrisch
ist, folgt aus Lemma 1.3 mit Hilfe von
(62), dass

Aus Lemma 3.8 ergibt sich nun eine Formel für den
Erwartungswert des in (60) betrachteten
ML-Schätzers
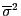 .
.
- Beweis
 Für den in (60) betrachteten
ML-Schätzer
Für den in (60) betrachteten
ML-Schätzer
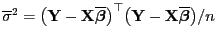 ergibt sich mit den in
Lemma 3.8 hergeleiteten Eigenschaften der Matrix
ergibt sich mit den in
Lemma 3.8 hergeleiteten Eigenschaften der Matrix
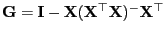 , dass
, dass

- Beachte
 Mit der Schreibweise
Mit der Schreibweise
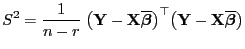 bzw. bzw.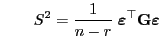 |
(64) |
ergibt sich aus Theorem 3.13, dass
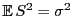 , d.h.,
, d.h., 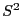 ist ein erwartungstreuer Schätzer für
ist ein erwartungstreuer Schätzer für
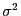 .
.
Um die Verteilungen der Schätzer
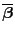 bzw.
bzw. 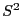 bestimmen zu können, benötigen wir den Begriff der singulären
multivariaten Normalverteilung, vgl. Abschnitt 1.2.5.
bestimmen zu können, benötigen wir den Begriff der singulären
multivariaten Normalverteilung, vgl. Abschnitt 1.2.5.
Theorem 3.14

Sei
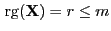
. Dann gilt
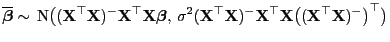 |
(65) |
und
 |
(66) |
wobei die Zufallsvariablen
und
unabhängig sind.
- Beweis
-




Nächste Seite: Tests linearer Hypothesen
Aufwärts: Normalverteilte Störgrößen
Vorherige Seite: Normalverteilte Störgrößen
Inhalt
Hendrik Schmidt
2006-02-27
![]() .
.
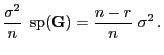
![]() bzw.
bzw. ![]() bestimmen zu können, benötigen wir den Begriff der singulären
multivariaten Normalverteilung, vgl. Abschnitt 1.2.5.
bestimmen zu können, benötigen wir den Begriff der singulären
multivariaten Normalverteilung, vgl. Abschnitt 1.2.5.