



Next: Stichprobenmittel
Up: Grundideen der statistischen Datenanalyse
Previous: Grundideen der statistischen Datenanalyse
Contents
Zufallsstichprobe
Der Vektor der vorliegenden Daten
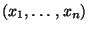 kann
natürlich im allgemeinen eine komplizierte Struktur aufweisen.
kann
natürlich im allgemeinen eine komplizierte Struktur aufweisen.
- Dabei muß der ,,Wert''
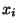 nicht unbedingt eine Zahl sein,
sondern
nicht unbedingt eine Zahl sein,
sondern 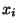 kann für jedes
kann für jedes
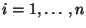 selbst ein Vektor
sein, der beispielsweise die Lage, Größe, Form und Orientierung
eines geometrischen Objektes beschreiben kann.
selbst ein Vektor
sein, der beispielsweise die Lage, Größe, Form und Orientierung
eines geometrischen Objektes beschreiben kann.
- Im Rahmen dieser einführenden Vorlesung setzen wir jedoch stets
voraus, daß
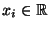 für jedes
für jedes
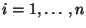 .
.
- Eine Ausnahme bilden lediglich die in den
Abschnitten 5.3.5 und 5.4.3 diskutierten
Zwei-Stichproben-Probleme, bei denen der Fall
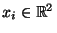 für
jedes
für
jedes
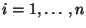 betrachtet wird.
betrachtet wird.
Wir nehmen an, daß die Daten
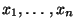 die Realisierung eines stochastischen Modells sind.
die Realisierung eines stochastischen Modells sind.
- Definition 5.1
-
- Der Vektor
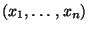 heißt (konkrete) Stichprobe.
heißt (konkrete) Stichprobe.
- Die Menge
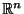 aller (potentiell möglichen) Stichproben
aller (potentiell möglichen) Stichproben
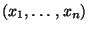 heißt Stichprobenraum.
heißt Stichprobenraum.
- Der Zufallsvektor
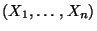 heißt Zufallsstichprobe.
heißt Zufallsstichprobe.
- Für jedes
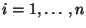 heißt
heißt 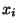 Stichprobenwert von
Stichprobenwert von
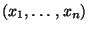 . Analog hierzu nennt man
. Analog hierzu nennt man  Stichprobenvariable von
Stichprobenvariable von
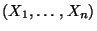 .
.
- Die Dimension
 von
von
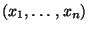 bzw.
bzw.
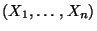 heißt Stichprobenumfang.
heißt Stichprobenumfang.
- Beachte
-
- Die allgemeine Zielstellung der statistischen Datenanalyse, die in der
Einleitung des Abschnittes 5.1 diskutiert wurde, kann
nun wie folgt präzisiert werden: Aus den vorliegenden
Daten
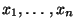 sollen Schlußfolgerungen über
Eigenschaften der (unbekannten) Verteilung der
Zufallsstichprobe
sollen Schlußfolgerungen über
Eigenschaften der (unbekannten) Verteilung der
Zufallsstichprobe
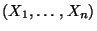 gezogen werden.
gezogen werden.
- Weil wir voraussetzen, daß die Stichprobenvariablen
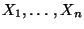 unabhängig und identisch verteilt
sind, wird die Verteilung von
unabhängig und identisch verteilt
sind, wird die Verteilung von
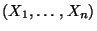 eindeutig durch die
(Rand-) Verteilungsfunktion
eindeutig durch die
(Rand-) Verteilungsfunktion 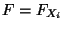 einer (einzelnen)
Stichprobenvariablen bestimmt, vgl.
Abschnitt 3.5.2.
einer (einzelnen)
Stichprobenvariablen bestimmt, vgl.
Abschnitt 3.5.2.
- Aus den Daten
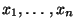 sollen also Schlußfolgerungen über
Eigenschaften der unbekannten Verteilungsfunktion
sollen also Schlußfolgerungen über
Eigenschaften der unbekannten Verteilungsfunktion 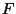 gezogen werden.
gezogen werden.
Um Eigenschaften der Verteilungsfunktion 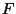 zu bestimmen, werden
Funktionen
zu bestimmen, werden
Funktionen
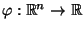 betrachtet, die der Stichprobe
betrachtet, die der Stichprobe
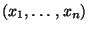 die ,,Bewertung''
die ,,Bewertung''
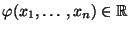 zuordnen, vgl. auch
Abschnitt 3.6.1. Dies führt zu der folgenden
Begriffsbildung.
zuordnen, vgl. auch
Abschnitt 3.6.1. Dies führt zu der folgenden
Begriffsbildung.
- Definition 5.2
 Eine Borel-meßbare Abbildung
Eine Borel-meßbare Abbildung
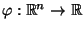 heißt Stichprobenfunktion.
heißt Stichprobenfunktion.
- Beachte
 Es ist üblich, auch die zusammengesetzte
Abbildung
Es ist üblich, auch die zusammengesetzte
Abbildung
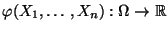 mit
mit
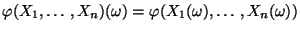 Stichprobenfunktion zu nennen, d.h.,
Stichprobenfunktion zu nennen, d.h., 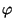 ist dann eine
Funktion der Zufallsstichprobe
ist dann eine
Funktion der Zufallsstichprobe
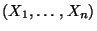 .
.




Next: Stichprobenmittel
Up: Grundideen der statistischen Datenanalyse
Previous: Grundideen der statistischen Datenanalyse
Contents
Roland Maier
2001-08-20
![]() kann
natürlich im allgemeinen eine komplizierte Struktur aufweisen.
kann
natürlich im allgemeinen eine komplizierte Struktur aufweisen.
![]() die Realisierung eines stochastischen Modells sind.
die Realisierung eines stochastischen Modells sind.
![]() zu bestimmen, werden
Funktionen
zu bestimmen, werden
Funktionen
![]() betrachtet, die der Stichprobe
betrachtet, die der Stichprobe
![]() die ,,Bewertung''
die ,,Bewertung''
![]() zuordnen, vgl. auch
Abschnitt 3.6.1. Dies führt zu der folgenden
Begriffsbildung.
zuordnen, vgl. auch
Abschnitt 3.6.1. Dies führt zu der folgenden
Begriffsbildung.