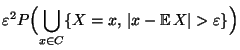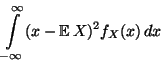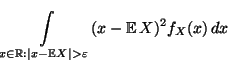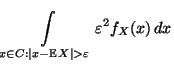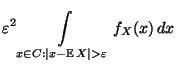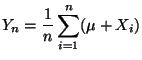Next: Gesetz der großen Zahlen
Up: Abschätzungen und Grenzwertsätze
Previous: Abschätzungen und Grenzwertsätze
Contents
Tschebyschewsche Ungleichung
In diesem Abschnitt wird die sogenannte Tschebyschewsche Ungleichung
diskutiert.
Sie liefert eine obere Schranke für die Wahrscheinlichkeit, daß
die Abweichungen
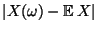 der Werte
der Werte 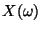 einer
Zufallsvariablen
einer
Zufallsvariablen  von ihrem Erwartungswert
von ihrem Erwartungswert
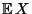 einen vorgegebenen
Schwellenwert
einen vorgegebenen
Schwellenwert
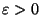 überschreiten.
überschreiten.
- Theorem 4.17
 Sei
Sei
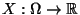 eine Zufallsvariable
mit
eine Zufallsvariable
mit
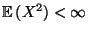 . Dann gilt für jedes
. Dann gilt für jedes
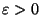
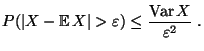 |
(40) |
- Beweis
-
- Korollar 4.18
 Sei
Sei
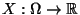 eine Zufallsvariable
mit
eine Zufallsvariable
mit
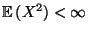 . Dann gilt
Var
. Dann gilt
Var 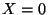 genau dann,
wenn
genau dann,
wenn
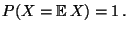 |
(41) |
- Beweis
-
- Falls
Var
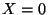 , dann ergibt sich aus
(40), daß
für jedes
, dann ergibt sich aus
(40), daß
für jedes
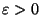 .
.
- Außerdem kann man sich leicht überlegen, daß dann
- Dies impliziert (41).
- Andererseits impliziert (41) die Gültigkeit von
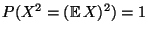 , d.h.,
, d.h., 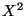 ist eine diskrete
Zufallsvariable.
ist eine diskrete
Zufallsvariable.
- Aus der Definitionsgleichung
(3) für den Erwartungswert diskreter
Zufallsvariablen ergibt sich dann, daß
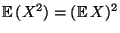 .
.
- Wegen (16) folgt hieraus, daß
Var
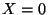 .
.
- Beachte
-
- Die Tschebyschewsche Ungleichung (40) ist nicht an
spezielle Annahmen über die Form der Verteilung der
Zufallsvariablen
 gebunden.
gebunden.
- Der ,,Preis'' hierfür ist, daß (40) in vielen
Fällen zu relativ groben Abschätzungen führt.
- Wenn zusätzliche Annahmen über die Verteilung
von
 gemacht werden, dann lassen sich
genauere Abschätzungen herleiten bzw. die Wahrscheinlichkeit
gemacht werden, dann lassen sich
genauere Abschätzungen herleiten bzw. die Wahrscheinlichkeit
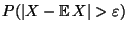 läßt sich explizit bestimmen.
läßt sich explizit bestimmen.
- Beispiele
-
- fehlerbehaftete Messungen
- Von einem Meßgerät sei bekannt, daß die
Meßergebnisse fehlerbehaftet sind.
- Die
 -te Messung einer (unbekannten) Größe
-te Messung einer (unbekannten) Größe
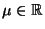 liefere den Wert
liefere den Wert
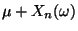 für
für
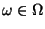 .
.
- Die Meßfehler
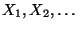 seien unabhängige und
identisch verteilte Zufallsvariable.
seien unabhängige und
identisch verteilte Zufallsvariable.
- Über die Verteilung von
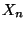 sei lediglich bekannt,
daß
sei lediglich bekannt,
daß
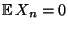 und Var und Var 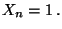 |
(42) |
- Es soll nun die Frage diskutiert werden,
wieviele Messungen erforderlich sind, um mit Hilfe
der Tschebyschewschen Ungleichung (40)
schlußfolgern zu können, daß das arithmetische Mittel
der zufälligen Meßwerte
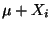 höchstens mit
Wahrscheinlichkeit
höchstens mit
Wahrscheinlichkeit 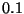 um mehr als
um mehr als 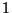 vom
,,wahren'', jedoch unbekannten Wert
vom
,,wahren'', jedoch unbekannten Wert 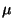 abweicht.
abweicht.
- Aus den Korollaren 4.6. und 4.8
ergibt sich, daß
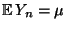
und Var
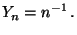
- Hieraus und aus der Tschebyschewschen Ungleichung
(40) ergibt sich, daß
- Es gilt also
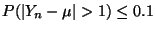 , falls
, falls
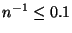 .
.
- Aus diesen Überlegungen folgt, daß
die obengenannten Genauigkeitsvorgaben erfüllt
sind, falls
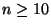 Messungen durchgeführt werden.
Messungen durchgeführt werden.
- normalverteilte Meßfehler
- Beachte
-
- Es gibt keine geschlossene Formel für die Stammfunktion
des Integrals in (43).
- Die Werte
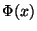 der Verteilungsfunktion der Standardnormalverteilung
müssen deshalb numerisch berechnet werden.
der Verteilungsfunktion der Standardnormalverteilung
müssen deshalb numerisch berechnet werden.
- Für
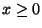 sind die Werte
sind die Werte 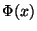 in Tabelle 1 gegeben.
in Tabelle 1 gegeben.
- Für
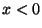 erhält man
erhält man 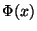 dann aus der folgenden
Symmetrieeigenschaft, die sich unmittelbar aus der
Definitionsgleichung (43) ergibt.
dann aus der folgenden
Symmetrieeigenschaft, die sich unmittelbar aus der
Definitionsgleichung (43) ergibt.
- Lemma 4.19
 Für jedes
Für jedes
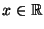 gilt
gilt
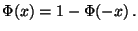 |
(44) |




Next: Gesetz der großen Zahlen
Up: Abschätzungen und Grenzwertsätze
Previous: Abschätzungen und Grenzwertsätze
Contents
Roland Maier
2001-08-20
![]() der Werte
der Werte ![]() einer
Zufallsvariablen
einer
Zufallsvariablen ![]() von ihrem Erwartungswert
von ihrem Erwartungswert
![]() einen vorgegebenen
Schwellenwert
einen vorgegebenen
Schwellenwert
![]() überschreiten.
überschreiten.