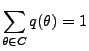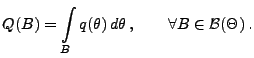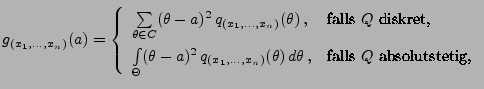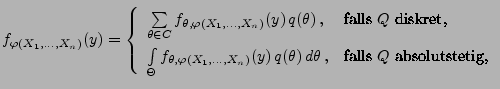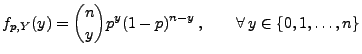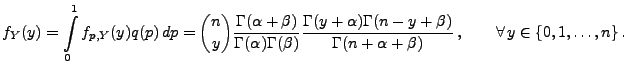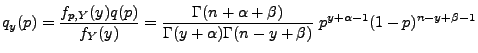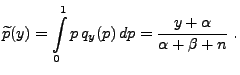Nächste Seite: Güteeigenschaften von Punktschätzern
Aufwärts: Methoden zur Gewinnung von
Vorherige Seite: Maximum-Likelihood-Schätzer
Inhalt
Bayes-Schätzer
- Zur Erinnerung: Bei der Momenten-Methode in
Abschnitt 2.2.1 und auch bei der
Maximum-Likelihood-Methode in Abschnitt 2.2.2
betrachteten wir das parametrische Modell, das in
Abschnitt 2.1 eingeführt worden ist.
- Dabei setzten wir voraus, dass die Verteilungsfunktion
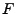 der
Stichprobenvariablen
der
Stichprobenvariablen
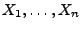 zu
einer vorgegebenen (d.h. bekannten) parametrischen Familie von
Verteilungsfunktionen
zu
einer vorgegebenen (d.h. bekannten) parametrischen Familie von
Verteilungsfunktionen
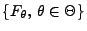 gehört.
gehört.
- Mit anderen Worten:
Es wurde angenommen, dass
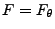 für ein
für ein
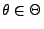 ,
wobei der Parametervektor
,
wobei der Parametervektor
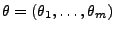 (bzw. ein Teil seiner Komponenten) unbekannt sei
und aus den beobachteten Daten
(bzw. ein Teil seiner Komponenten) unbekannt sei
und aus den beobachteten Daten
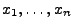 geschätzt
werden soll.
geschätzt
werden soll.
- Wir modifizieren nun dieses parametrische Modell folgendermaßen.
- Anstelle der bisherigen Modellannahme, dass der Parameter
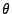 ein zwar unbekannter, jedoch deterministischer Vektor ist, setzen
wir jetzt voraus, dass der Parameter selbst ein Zufallsvektor ist,
den wir mit
ein zwar unbekannter, jedoch deterministischer Vektor ist, setzen
wir jetzt voraus, dass der Parameter selbst ein Zufallsvektor ist,
den wir mit
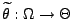 bezeichnen.
bezeichnen.
- Dabei nehmen wir an, dass wir bereits (vor der Erhebung von Daten)
eine gewisse Vorkenntnis über die Verteilung von
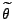 besitzen.
besitzen.
- Diese Vorkenntnis modellieren wir durch eine Verteilung
![% latex2html id marker 26897
$ Q:\mathcal{B}(\Theta)\to[0,1]$](img802.png) über dem Parameterraum
über dem Parameterraum
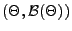 , die wir a-priori-Verteilung von
, die wir a-priori-Verteilung von
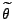 nennen.
nennen.
- Beachte
-
- Definition
 (a-posteriori-Verteilung)
(a-posteriori-Verteilung)
- Beachte
 Die Funktion
Die Funktion
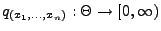 kann als
bedingte Wahrscheinlichkeitsfunktion bzw. bedingte Dichte von
kann als
bedingte Wahrscheinlichkeitsfunktion bzw. bedingte Dichte von
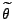 angesehen werden, unter der Bedingung, dass
angesehen werden, unter der Bedingung, dass
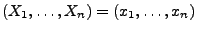 , denn
, denn
- die Likelihood-Funktion
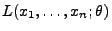 können wir als
bedingte Wahrscheinlichkeitsfunktion bzw. bedingte Dichte von
können wir als
bedingte Wahrscheinlichkeitsfunktion bzw. bedingte Dichte von
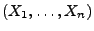 ansehen, unter der Bedingung, dass
ansehen, unter der Bedingung, dass
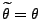 ,
,
- das Produkt
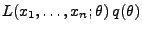 als die
gemeinsame (unbedingte) Wahrscheinlichkeitsfunktion bzw. Dichte
des Zufallsvektors
als die
gemeinsame (unbedingte) Wahrscheinlichkeitsfunktion bzw. Dichte
des Zufallsvektors
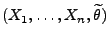 , und
, und
- die in (18) gegebene Funktion
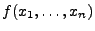 als die (Rand-) Wahrscheinlichkeitsfunktion bzw. Dichte von
als die (Rand-) Wahrscheinlichkeitsfunktion bzw. Dichte von
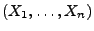 .
.
- Definition
 (Bayes-Schätzer)
Man kann zeigen (vgl. Übungsaufgabe WR-8.3), dass der in
(20) gegebene Schätzwert
(Bayes-Schätzer)
Man kann zeigen (vgl. Übungsaufgabe WR-8.3), dass der in
(20) gegebene Schätzwert
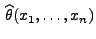 den mittleren
quadratischen Fehler
minimiert, d.h., es gilt
den mittleren
quadratischen Fehler
minimiert, d.h., es gilt
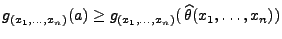 für jedes
für jedes
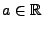 , vgl. auch Abschnitt 2.3.1.
, vgl. auch Abschnitt 2.3.1.
- Beachte
-
- Beispiel
 (Bernoulli-verteilte
Stichprobenvariablen)
(Bernoulli-verteilte
Stichprobenvariablen)
- Betrachten die Familie
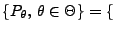 Bin
Bin
![$ (1,p),\,p\in[0,1]\}$](img738.png) der Bernoulli-Verteilungen.
der Bernoulli-Verteilungen.
- Die a-priori-Verteilung von
![$ \widetilde p:\Omega\to[0,1]$](img837.png) sei die
Betaverteilung Beta
sei die
Betaverteilung Beta
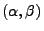 , wobei die Parameter
, wobei die Parameter
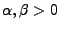 vorgegeben seien.
vorgegeben seien.
- Die a-priori-Dichte
![$ q:[0,1]\to(0,\infty)$](img840.png) von
von
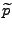 ist
also gegeben durch
ist
also gegeben durch
![$\displaystyle q(p)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}p^{\alpha-1}(1-p)^{\beta-1}\,,
\qquad\forall\,p\in[0,1]\,.$](img842.png) |
(22) |
- Wir betrachten die Stichprobenfunktion
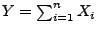 , d.h.,
, d.h.,
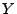 ist die Anzahl der ,,Erfolge'' bei
ist die Anzahl der ,,Erfolge'' bei 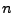 Versuchen.
Versuchen.
- Dann gilt für jedes
![$ p\in[0,1]$](img844.png) und somit
und somit
- Für die a-posteriori Dichte
![$ q_{y}:[0,1]\to[0,\infty)$](img847.png) von
von
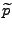 ergibt sich hieraus, dass
für beliebige
ergibt sich hieraus, dass
für beliebige
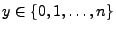 und
und ![$ p\in[0,1]$](img844.png) .
.
- Dies ist die Dichte der Betaverteilung Beta
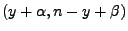 .
.
- Für den Erwartungswert
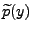 dieser Verteilung gilt
dieser Verteilung gilt
- Dies ergibt den Bayes-Schätzer
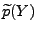 mit
bzw.
mit
bzw.
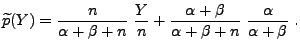 |
(23) |
- Der Bayes-Schätzer
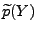 ist also eine
Linearkombination
ist also eine
Linearkombination
- des Erwartungswertes
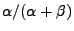 der
a-priori-Verteilung von
der
a-priori-Verteilung von
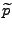 , der ein natürlicher
Schätzer wäre, wenn wir über keinerlei Daten verfügen würden, und
, der ein natürlicher
Schätzer wäre, wenn wir über keinerlei Daten verfügen würden, und
- des Stichprobenmittels
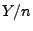 , das ein natürlicher Schätzer wäre,
wenn keine a-priori-Verteilung von
, das ein natürlicher Schätzer wäre,
wenn keine a-priori-Verteilung von
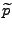 zur Verfügung
stehen würde.
zur Verfügung
stehen würde.




Nächste Seite: Güteeigenschaften von Punktschätzern
Aufwärts: Methoden zur Gewinnung von
Vorherige Seite: Maximum-Likelihood-Schätzer
Inhalt
Ursa Pantle
2004-07-14