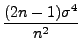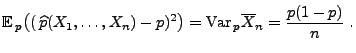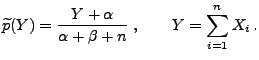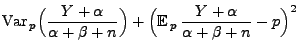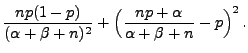- Es gelte
wobei
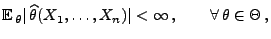
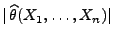 die Länge des
Zufallsvektors
die Länge des
Zufallsvektors
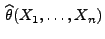 bezeichnet.
bezeichnet.
- Dann heißt der Schätzer
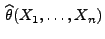
- erwartungstreu, falls
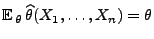 für jedes
für jedes
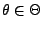 ,
,
- asymptotisch erwartungstreu, falls
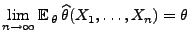 für jedes
für jedes
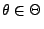 .
.
- erwartungstreu, falls
- Die Verzerrung bzw. der Bias von
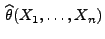 unter
unter 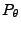 ist die
Differenz
ist die
Differenz
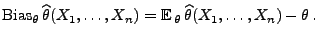
- Falls
dann heißt der Erwartungswert
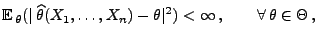
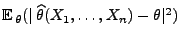 die mittlere
quadratische Abweichung des Schätzers
die mittlere
quadratische Abweichung des Schätzers
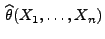 von dem zu schätzenden
Parametervektor
von dem zu schätzenden
Parametervektor
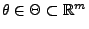 .
.
- Anstelle ,,mittlere quadratische Abweichung'' sagen wir auch kurz
MQ-Fehler von
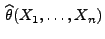 .
.
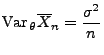 bzw.
bzw.