



Next: Konfidenzbereiche; Prognose von Zielvariablen
Up: Normalverteilte Störgrößen
Previous: Verteilungs- und Unabhängigkeitseigenschaften linearer
Contents
Tests für die Regressionskoeffizienten;
Quadratsummenzerlegung
- Mit Hilfe der Verteilungs- und Unabhängigkeitseigenschaften von
linearen bzw. quadratischen Formen normalverteilter
Zufallsvektoren, die in den Abschnitten 3.3.2 -
3.3.4 hergeleitet wurden, kann man t-Tests bzw.
F-Tests zur Verifizierung von Hypothesen über die
Regressionskoeffizienten
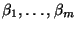 konstruieren.
konstruieren.
- Zur Erinnerung: Es gilt
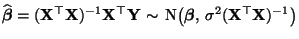 |
(77) |
bzw.
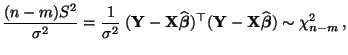 |
(78) |
wobei die Zufallsvariablen
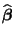 und
und 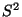 unabhängig
sind.
unabhängig
sind.
Zunächst testen wir Hypothesen über einzelne Komponenten des
Parametervektors
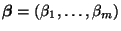 .
.
- Beachte
-
Auf ähnliche Weise ergibt sich der folgende (simultane) F-Test,
der auch Test auf Gesamtzusammenhang bzw. Test auf
Signifikanz des Modells genannt wird.
- Dabei wird die Hypothese
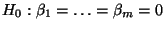 (gegen die
Alternative
(gegen die
Alternative
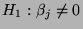 für ein
für ein
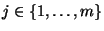 )
getestet.
)
getestet.
- Die Wahl der Testgröße ist durch die folgende Quadratsummenzerlegung motiviert; vgl. auch
Abschnitt 2.2.4.
- Beweis
-
- Es gilt
- Dabei ergibt sich die vorletzte Gleichheit aus der folgenden
Überlegung: Wegen (77) gilt
und somit

- Beachte
-
- Der erste Summand
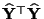 auf der
rechten Seite von (82) ist die quadrierte Länge des
Vektors
auf der
rechten Seite von (82) ist die quadrierte Länge des
Vektors
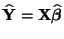 der durch die
Regression geschätzten Zielwerte
der durch die
Regression geschätzten Zielwerte
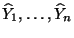 .
.
- Die zweite Komponente der Quadratsummenzerlegung
(82), d.h. die Summe der Abweichungsquadrate
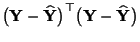 wird manchmal auch Reststreuung genannt.
wird manchmal auch Reststreuung genannt.
- Aus unserer generellen Modellannahme, daß die Designmatrix
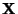 vollen Rang hat, d.h.
vollen Rang hat, d.h.
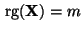 , ergibt sich die Ungleichung
falls die Hypothese
, ergibt sich die Ungleichung
falls die Hypothese
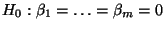 falsch ist.
falsch ist.
- Deshalb ist es naheliegend, die Hypothese
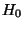 abzulehnen, falls
die quadrierte Länge
abzulehnen, falls
die quadrierte Länge
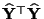 des
Zufallsvektors
des
Zufallsvektors
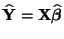 hinreichend
groß ist.
hinreichend
groß ist.
- Dabei wird bei der Entscheidung, was ,,hinreichend groß'' ist,
auch die Variabilität der Daten berücksichtigt, d.h., es wird der
Quotient von
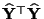 und der Summe der
Abweichungsquadrate
und der Summe der
Abweichungsquadrate
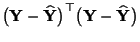 betrachtet.
betrachtet.
- Genauer gesagt: Wir betrachten die folgende Testgröße
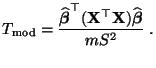 |
(83) |
- Um einen auf
 basierenden Test der Hypothese
basierenden Test der Hypothese
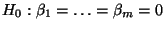 konstruieren zu können, muß
zunächst die Verteilung der Testgröße
konstruieren zu können, muß
zunächst die Verteilung der Testgröße
 bestimmt
werden.
bestimmt
werden.
Theorem 3.18

Unter
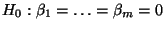
gilt
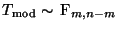
, d.h., die in
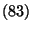
gegebene Testgröße

ist F-verteilt mit
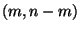
Freiheitsgraden.
- Beweis
-
- Beachte
-
Die bisher in diesem Abschnitt betrachteten Tests sind
Spezialfälle des folgenden universellen Tests. Dabei wird
lediglich ein Teil der Komponenten des Parametervektors
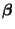 getestet.
getestet.
- Seien
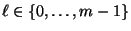 und
und
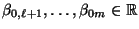 beliebige, jedoch fest
vorgegebene Zahlen.
beliebige, jedoch fest
vorgegebene Zahlen.
- Es soll nun die Hypothese
getestet werden.
- Hierfür betrachten wir die folgende
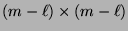 -dimensionale Teilmatrix
-dimensionale Teilmatrix
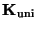 der Matrix
der Matrix
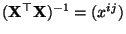 mit
mit
- Außerdem betrachten wir den Teilvektor
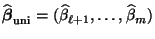 des
Zufallsvektors
des
Zufallsvektors
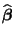 .
.
- Ein Ansatz zur Lösung des Testproblems (87) ist
durch die Testgröße
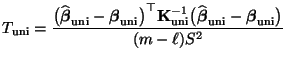 |
(88) |
gegeben, wobei
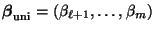 .
.
- Man kann nämlich zeigen, daß unter der in (87)
formulierten Nullhypothese
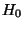
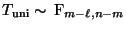 |
(89) |
gilt (vgl. Übungsaufgabe 9.2 bzw. das folgende
Theorem 3.19). Die Hypothese
wird somit abgelehnt, falls
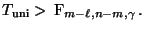 |
(90) |
Wir diskutieren nun noch einen Test für Linearformen des
Parametervektors
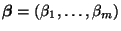 , der eine
weitere Verallgemeinerung der bisher in diesem Abschnitt
betrachteten Tests ist.
, der eine
weitere Verallgemeinerung der bisher in diesem Abschnitt
betrachteten Tests ist.
Lemma 3.15
- Seien
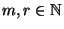 beliebige natürliche Zahlen mit
beliebige natürliche Zahlen mit
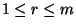 .
Sei
.
Sei
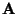 eine symmetrische und positiv definite
eine symmetrische und positiv definite 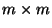 Matrix, und sei
Matrix, und sei
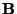 eine
eine 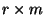 Matrix mit vollem Rang
Matrix mit vollem Rang
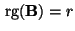 .
.
- Dann sind auch die Matrizen
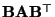 und
und
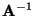 positiv definit.
positiv definit.
- Beweis
-
Theorem 3.19

Unter
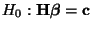
gilt
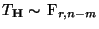
, d.h., die in
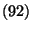
gegebene Testgröße
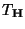
ist F-verteilt mit
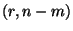
Freiheitsgraden.
- Beweis
-
- Beachte
 Die Nullhypothese
Die Nullhypothese
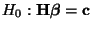 wird abgelehnt, falls
wird abgelehnt, falls
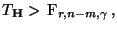 |
(93) |
wobei
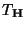 die in
die in
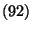 gegebene Testgröße
ist.
gegebene Testgröße
ist.




Next: Konfidenzbereiche; Prognose von Zielvariablen
Up: Normalverteilte Störgrößen
Previous: Verteilungs- und Unabhängigkeitseigenschaften linearer
Contents
Ursa Pantle
2003-03-10
![]() .
.
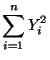
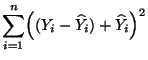
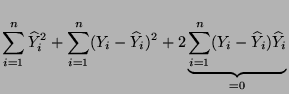
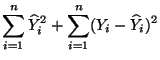
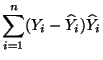
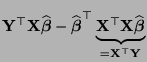
![]() getestet.
getestet.
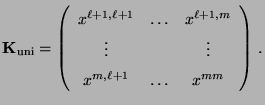
![]() , der eine
weitere Verallgemeinerung der bisher in diesem Abschnitt
betrachteten Tests ist.
, der eine
weitere Verallgemeinerung der bisher in diesem Abschnitt
betrachteten Tests ist.