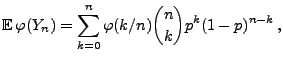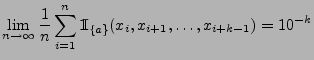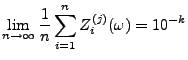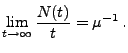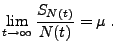- Betrachten das System
von parallelen und äquidistanten (vertikalen) Geraden in der euklidischen Ebene
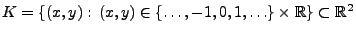
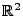 ; vgl. auch
Abschnitt 2.5.
; vgl. auch
Abschnitt 2.5.
- Werfen eine Nadel mit der Länge 1
,,willkürlich'' in die Ebene
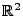 , wobei
mit ,,willkürlich'' das folgende
stochastische Modell gemeint ist.
, wobei
mit ,,willkürlich'' das folgende
stochastische Modell gemeint ist.
- Betrachten zwei Zufallsvariablen
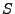 und
und 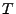 ,
die die zufällige Lage der Nadel beschreiben, wobei
,
die die zufällige Lage der Nadel beschreiben, wobei
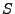 der (orthogonale) Abstand des Nadelmittelpunktes
zur nächsten linksliegenden Nachbargeraden von
der (orthogonale) Abstand des Nadelmittelpunktes
zur nächsten linksliegenden Nachbargeraden von 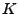 ist,
ist,
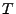 der Winkel ist, den die Nadel zum Lot auf die
Geraden von
der Winkel ist, den die Nadel zum Lot auf die
Geraden von 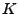 bildet, und
bildet, und
- die Zufallsvariablen
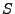 und
und 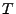 unabhängig und gleichverteilt seien auf den Intervallen
unabhängig und gleichverteilt seien auf den Intervallen
![$ [0,1]$](img1917.png) bzw.
bzw.
![$ [-\pi/2,\pi/2]$](img1918.png) .
.
- Bestimmen die Wahrscheinlichkeit des
Ereignisses
dass die willkürlich geworfene Nadel eine der Geraden von
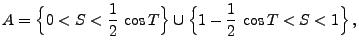
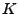 schneidet.
schneidet.
- Es gilt
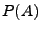
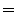
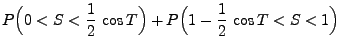
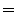
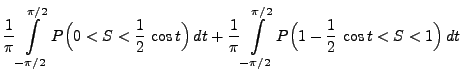
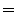
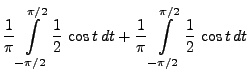
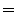
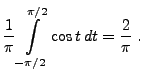
- Aus der Gleichung
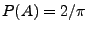 ergibt sich nun eine Methode zur
experimentellen Bestimmung der Zahl
ergibt sich nun eine Methode zur
experimentellen Bestimmung der Zahl 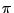 , die auf dem Gesetz der
großen Zahlen beruht.
, die auf dem Gesetz der
großen Zahlen beruht.
- Seien
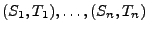 unabhängige und
identisch verteilte Zufallsvektoren (mit der gleichen
Verteilung wie
unabhängige und
identisch verteilte Zufallsvektoren (mit der gleichen
Verteilung wie 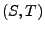 ), die wir als
das Ergebnis von
), die wir als
das Ergebnis von  (unabhängig durchgeführten) Nadelexperimenten auffassen.
(unabhängig durchgeführten) Nadelexperimenten auffassen.
- Dann sind
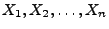 mit
unabhängige und identisch verteilte Zufallsvariablen mit dem Erwartungswert
mit
unabhängige und identisch verteilte Zufallsvariablen mit dem Erwartungswert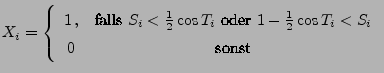
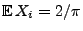 .
.
- Aus Theorem 5.15 ergibt sich also, dass das
arithmetische Mittel
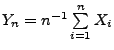 fast sicher gegen die Zahl
fast sicher gegen die Zahl 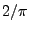 strebt.
strebt.
- D.h., für große
 ist
ist 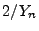 mit
hoher Wahrscheinlichkeit eine gute Näherung der Zahl
mit
hoher Wahrscheinlichkeit eine gute Näherung der Zahl
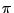 .
.
- Ein einfacher Algorithmus zur Monte-Carlo-Simulation der Zahl
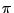 hängt mit dem folgenden geometrischen Sachverhalt
zusammen.
hängt mit dem folgenden geometrischen Sachverhalt
zusammen.
- Betrachten das Quadrat
und den Kreis
![$\displaystyle B=[-1,1]\times[-1,1]\subset\mathbb{R}^2
$](img1931.png)
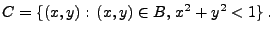
- Werfen einen Punkt willkürlich in die Menge
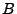 .
.
- D.h., wir betrachten zwei unabhängige
Zufallsvariablen
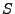 und
und 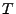 , die jeweils
gleichverteilt auf dem Intervall
, die jeweils
gleichverteilt auf dem Intervall ![$ [-1,1]$](img1933.png) sind.
sind.
- Bestimmen die Wahrscheinlichkeit des Ereignisses
dass der ,,zufällige Punkt''
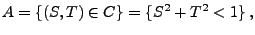
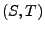 in
in
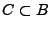 liegt.
liegt.
- Es gilt
wobei
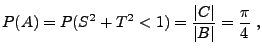
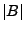 ,
, 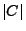 den Flächeninhalt von
den Flächeninhalt von 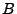 bzw.
bzw.
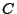 bezeichnet.
bezeichnet.
- Ähnlich wie beim Buffonschen Nadelexperiment
ergibt sich nun aus der Gleichung
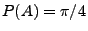 eine weitere Methode zur experimentellen Bestimmung der Zahl
eine weitere Methode zur experimentellen Bestimmung der Zahl 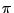 ,
die auf dem Gesetz der großen Zahlen beruht und
die sich leicht implementieren lässt.
,
die auf dem Gesetz der großen Zahlen beruht und
die sich leicht implementieren lässt.
- Seien
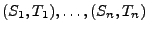 unabhängige und
identisch verteilte Zufallsvektoren (mit der gleichen
Verteilung wie
unabhängige und
identisch verteilte Zufallsvektoren (mit der gleichen
Verteilung wie 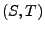 ), die wir als
das Ergebnis von
), die wir als
das Ergebnis von  (unabhängig durchgeführten) Experimenten auffassen.
(unabhängig durchgeführten) Experimenten auffassen.
- Dann sind
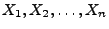 mit
unabhängige und identisch verteilte Zufallsvariablen mit dem Erwartungswert
mit
unabhängige und identisch verteilte Zufallsvariablen mit dem Erwartungswert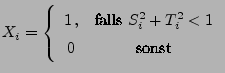
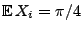 .
.
- Aus Theorem 5.15 ergibt sich also, dass das
arithmetische Mittel
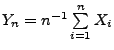 fast sicher gegen die Zahl
fast sicher gegen die Zahl 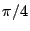 strebt.
strebt.
- D.h., für große
 ist
ist 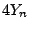 mit
hoher Wahrscheinlichkeit eine gute Näherung der Zahl
mit
hoher Wahrscheinlichkeit eine gute Näherung der Zahl
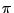 .
.
- Beachte:
Bei der Implementierung dieser Monte-Carlo-Simulation
kann man wie folgt vorgehen.
- Erzeuge
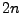 auf
auf ![$ [0,1]$](img1917.png) gleichverteilte Pseudozufallszahlen
gleichverteilte Pseudozufallszahlen
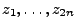 mit einem
Zufallszahlengenerator.
mit einem
Zufallszahlengenerator.
- Setze
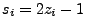 und
und
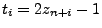 für
für
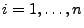 .
.
- Setze
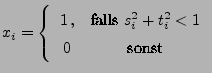
- Berechne
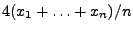 .
.
- Erzeuge
- Ein JAVA-Applet, mit dem dieses Simulationsverfahren selbst durchgeführt werden kann, findet man beispielsweise auf der Internet-Seite:
- Sei
![$ \varphi:[0,1]\to[0,1]$](img1951.png) eine stetige Funktion.
eine stetige Funktion.
- Mittels Monte-Carlo-Simulation soll der Wert des Integrals
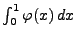 bestimmt werden.
bestimmt werden.
- Seien
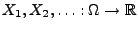 unabhängige und identisch
verteilte Zufallsvariable, die auf dem Intervall
unabhängige und identisch
verteilte Zufallsvariable, die auf dem Intervall ![$ [0,1]$](img1917.png) gleichverteilt sind.
gleichverteilt sind.
- Außerdem sei
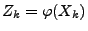 für jedes
für jedes
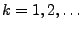 .
.
- Wegen Theorem 3.18 sind dann auch
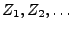 unabhängige und identisch verteilte Zufallsvariable,
unabhängige und identisch verteilte Zufallsvariable,
- und es gilt
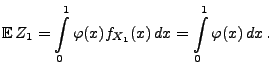
- Aus dem starken Gesetz der großen Zahlen (vgl.
Theorem 5.15) ergibt sich nun, dass für
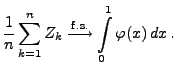
- D.h., für große
 ist
ist
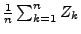 mit
hoher Wahrscheinlichkeit eine gute Näherung des
Integrals
mit
hoher Wahrscheinlichkeit eine gute Näherung des
Integrals
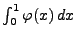 .
.
- Beachte:
Bei der Implementierung dieser Monte-Carlo-Simulation
kann man wie folgt vorgehen.
- Erzeuge
 auf
auf ![$ [0,1]$](img1917.png) gleichverteilte Pseudozufallszahlen
gleichverteilte Pseudozufallszahlen
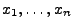 mit einem
Zufallszahlengenerator.
mit einem
Zufallszahlengenerator.
- Setze
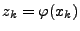 für
für
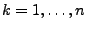
- Berechne
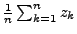 .
.
- Erzeuge
- Sei
![$ \varphi:[0,1]\to[0,1]$](img1951.png) eine stetige (und somit beschränkte)
Funktion.
eine stetige (und somit beschränkte)
Funktion.
- Mit Hilfe des starken Gesetzes der großen Zahlen (vgl.
Theorem 5.15) zeigen wir, dass sich die Funktion
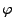 gleichmäßig durch Polynome approximieren lässt.
gleichmäßig durch Polynome approximieren lässt.
- Seien
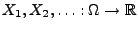 unabhängige und identisch
verteilte Zufallsvariablen mit
unabhängige und identisch
verteilte Zufallsvariablen mit 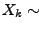 Bin
Bin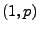 , wobei
, wobei
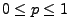 .
.
- Aus Theorem 5.15 folgt dann, dass
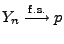 ,
wobei
,
wobei
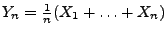 .
.
- Wir zeigen nun, dass darüber hinaus für
gleichmäßig in![$ p\in[0,1]$](img1090.png) gilt.
gilt.
- Für
 sei
sei 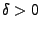 so gewählt, dass
so gewählt, dass
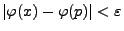 , falls
, falls
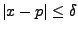 .
.
- Mit der Schreibweise
![$ b=\sup_{x\in[0,1]}\varphi(x)$](img1969.png) gilt dann die
Abschätzung
gilt dann die
Abschätzung
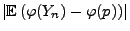
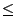
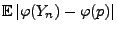
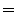
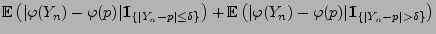
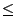
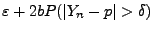
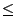
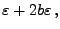
wobei sich die letzte Ungleichung aus der Tschebyschew-Ungleichung (4.72) ergibt. - Denn wegen (4.72) gilt (gleichmäßig in
![$ p\in[0,1]$](img1090.png) )
für jedes hinreichend große
)
für jedes hinreichend große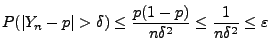
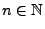 .
.
- Damit ist (34) bewiesen, weil
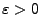 beliebig klein gewählt werden kann.
beliebig klein gewählt werden kann.
- Weil
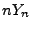 binomialverteilt ist, gilt
binomialverteilt ist, gilt
und diese Polynome in![$ p\in[0,1]$](img1090.png) konvergieren wegen
(34) gleichmäßig in
konvergieren wegen
(34) gleichmäßig in ![$ p\in[0,1]$](img1090.png) gegen
gegen
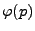 .
.
- Beachte: Die Polynome in (35) werden Bernstein-Polynome genannt.
- Wir betrachten den Wahrscheinlichkeitsraum
![$ (\Omega,\mathcal{F},P)=([0,1],\mathcal{B}([0,1]),P)$](img1979.png) , wobei
, wobei 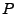 die
Gleichverteilung auf
die
Gleichverteilung auf
![$ \mathcal{B}([0,1])$](img1980.png) sei.
sei.
- Die Dezimalbruchentwicklung
ist (bis auf eine abzählbare Ausnahmemenge) für fast jedes
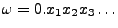
![$ \omega\in[0,1]$](img1982.png) eindeutig festgelegt.
eindeutig festgelegt.
- Dabei heißt
![$ \omega\in[0,1]$](img1982.png) normal, wenn in der
Dezimalbruchentwicklung
jede endliche Ziffernfolge
normal, wenn in der
Dezimalbruchentwicklung
jede endliche Ziffernfolge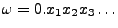
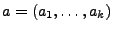 mit der relativen
Häufigkeit
mit der relativen
Häufigkeit 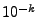 vorkommt.
vorkommt.
- Wir zeigen, dass fast jede Zahl
![$ \omega\in[0,1]$](img1982.png) normal ist,
normal ist,
- d.h., dass für jedes
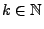 und für jedes
und für jedes
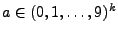
für fast jedes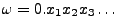 gilt.
gilt.
- Sei
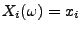 die
die 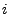 -te Ziffer in der
Dezimalbruchentwicklung von
-te Ziffer in der
Dezimalbruchentwicklung von 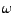 .
.
- Weil für jedes
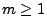 und jedes
und jedes
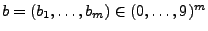 die Menge
ein Intervall der Länge
die Menge
ein Intervall der Länge![$\displaystyle \{X_1=b_1,\ldots,X_m=b_m\}\subset[0,1]
$](img1991.png)
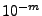 ist, gilt
ist, gilt
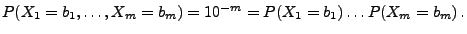
- Deshalb sind
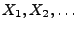 unabhängige und identisch verteilte
Zufallsvariable, deren Verteilung die (diskrete) Gleichverteilung
auf
unabhängige und identisch verteilte
Zufallsvariable, deren Verteilung die (diskrete) Gleichverteilung
auf
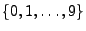 ist.
ist.
- Aus Theorem 5.15 ergibt sich dann sofort die
Gültigkeit von (36) für
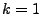 .
.
- Sei nun
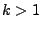 .
.
- Für
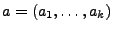 , für
, für
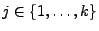 und für
und für 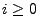 setzen wir
setzen wir
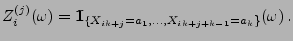
- Für jedes
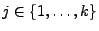 sind
sind
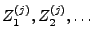 unabhängige (wegen Theorem 3.18) und identisch
verteilte Zufallsvariablen mit
und somit
unabhängige (wegen Theorem 3.18) und identisch
verteilte Zufallsvariablen mit
und somit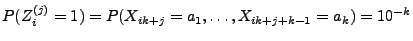
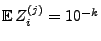 .
.
- Aus Theorem 5.15 ergibt sich also, dass
für jedes![$ \omega\in[0,1]\setminus
B_j(a)$](img2004.png) , wobei
, wobei
![$ B_j(a)\in\mathcal{B}([0,1])$](img2005.png) eine Ausnahmemenge ist mit
eine Ausnahmemenge ist mit
- Für jedes
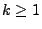 gibt es nur endlich viele
gibt es nur endlich viele 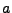 und endlich viele
und endlich viele
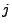 .
.
- Weil deshalb
die Vereinigung von abzählbar vielen Mengen ist, ergibt sich aus (38), dass auch
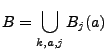
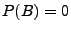 .
.
- Wegen (37) gilt nun
für beliebige
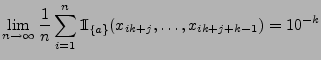
 ,
, 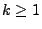 ,
,
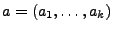 und
und
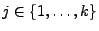 .
.
- Hieraus folgt, dass
für beliebige
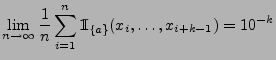
 ,
, 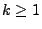 und
und
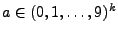 .
.
- Seien
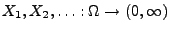 unabhängige und
identisch verteilte Zufallsvariable, die nur positive Werte
annehmen können;
unabhängige und
identisch verteilte Zufallsvariable, die nur positive Werte
annehmen können;
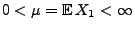 .
.
- Die Zufallsvariable
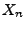 kann man als Modell für die zufällige
Zeitdauer deuten, die zwischen dem
kann man als Modell für die zufällige
Zeitdauer deuten, die zwischen dem 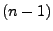 -ten und
-ten und  -ten
Eintreten eines biologischen, ökonomischen oder technischen
Systems in einen bestimmten (kritischen) Systemzustand vergeht.
-ten
Eintreten eines biologischen, ökonomischen oder technischen
Systems in einen bestimmten (kritischen) Systemzustand vergeht.
- Im Englischen spricht man dann von interoccurrence time.
- Beispielsweise kann
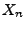 die zufällige Zeitdauer zwischen dem
die zufällige Zeitdauer zwischen dem
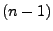 -ten und
-ten und  -ten Ausfallzeitpunkt eines technischen Systems
sein.
-ten Ausfallzeitpunkt eines technischen Systems
sein.
- Falls das System unmittelbar nach jedem Ausfall vollständig
repariert wird, dann kann man
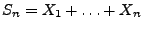 als den
als den  -ten
Erneuerungszeitpunkt des Systems auffassen.
-ten
Erneuerungszeitpunkt des Systems auffassen.
- Für jedes
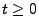 ist
ist
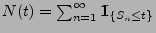 die zufällige Anzahl von Erneuerungen im Intervall
die zufällige Anzahl von Erneuerungen im Intervall ![$ (0,t]$](img2017.png) .
.
- Die Familie
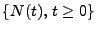 von Zufallsvariablen heißt Erneuerungszählprozess.
von Zufallsvariablen heißt Erneuerungszählprozess.
- Aus Theorem 5.15 folgt, dass mit
Wahrscheinlichkeit 1
- Dies ergibt sich aus den folgenden Überlegungen.
- Für jedes
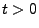 gilt
gilt
denn aus Theorem 5.15 folgt, dass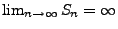 mit Wahrscheinlichkeit 1.
mit Wahrscheinlichkeit 1.
- Beachte. Man kann (40) auch auf direktem Wege
beweisen, denn es gilt
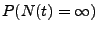
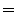
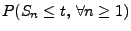
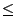
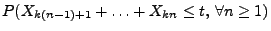
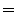
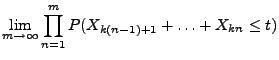
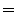
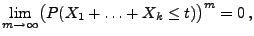
weil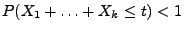 für jedes hinreichend große
für jedes hinreichend große
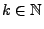 .
.
- Außerdem ist
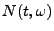 für jedes
für jedes
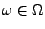 monoton
nichtfallend in
monoton
nichtfallend in 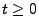 , d.h., der Grenzwert
, d.h., der Grenzwert
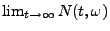 existiert für jedes
existiert für jedes
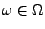 .
.
- Darüber hinaus gilt mit Wahrscheinlichkeit 1
weil
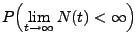
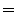
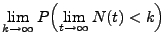
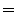
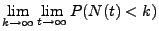
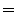
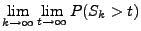
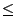
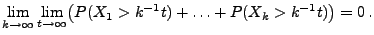
- Aus Theorem 5.15 folgt also, dass mit
Wahrscheinlichkeit 1
- Außerdem gilt für beliebige
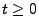 und
und
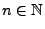
- Folglich gilt
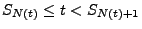 bzw.
bzw.
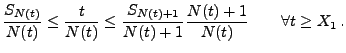
- Hieraus und aus (42) ergibt sich nun die Gültigkeit von (39).