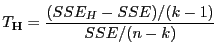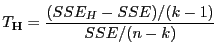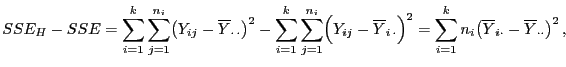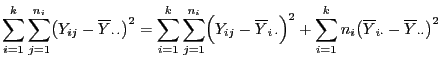Nächste Seite: F-Tests für die zweifaktorielle
Aufwärts: Beispiele
Vorherige Seite: Beispiele
Inhalt
F-Test der ANOVA-Nullhypothese
- Wir betrachten das reparametrisierte Modell der einfaktoriellen Varianzanalyse, d.h., die Designmatrix
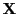 sei die in (13) gegebene
sei die in (13) gegebene
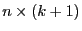 Matrix mit
Matrix mit
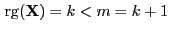 , wobei
, wobei
 |
(82) |
und der Parametervektor
 hat die Form
hat die Form
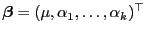 .
.
- Getestet werden soll, ob die Stufen des Einflussfaktors
signifikant sind, d.h., wir testen die ANOVA-Nullhypothese
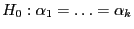 (gegen die Alternative
(gegen die Alternative
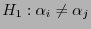 für ein Paar
für ein Paar
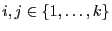 mit
mit 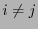 ). Dabei nutzen wir den allgemeinen Testansatz von
Theorem 3.15 bzw. Theorem 3.16.
). Dabei nutzen wir den allgemeinen Testansatz von
Theorem 3.15 bzw. Theorem 3.16.
- Eine äquivalente Formulierung der Nullhypothese
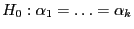 ist gegeben durch
ist gegeben durch
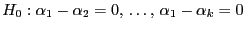 bzw. bzw.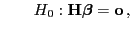 |
(83) |
wobei
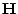 eine
eine
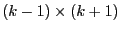 Matrix ist mit
Matrix ist mit
 |
(84) |
- Es ist klar, dass
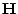 eine Matrix mit vollem Zeilenrang
eine Matrix mit vollem Zeilenrang
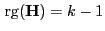 ist. Aus Theorem 3.10 ergibt sich
außerdem, dass sämtliche Komponenten
ist. Aus Theorem 3.10 ergibt sich
außerdem, dass sämtliche Komponenten
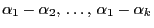 des Vektors
des Vektors
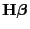 schätzbare Funktionen von
schätzbare Funktionen von
 sind.
sind.
- Mit anderen Worten: Die Matrix
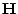 genügt den Bedingungen von
Theorem 3.15 bzw. Theorem 3.16, so dass
zur Verifizierung der Hypothese
genügt den Bedingungen von
Theorem 3.15 bzw. Theorem 3.16, so dass
zur Verifizierung der Hypothese
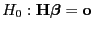 die in
Theorem 3.16 betrachtete Testgröße
verwendet werden kann, wobei sich die in (74) bzw.
(75) definierten Quadratsummen
die in
Theorem 3.16 betrachtete Testgröße
verwendet werden kann, wobei sich die in (74) bzw.
(75) definierten Quadratsummen 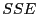 und
und 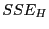 wie folgt bestimmen lassen.
wie folgt bestimmen lassen.
- Zur Erinnerung: In Abschnitt 3.2.1 hatten wir
gezeigt, dass eine verallgemeinerte Inverse von
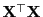 gegeben ist durch (35), d.h.
gegeben ist durch (35), d.h.
 |
(85) |
- Hieraus und aus (82) folgt, dass
bzw.
- Somit ergibt sich für die Quadratsumme
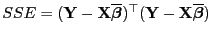 ,
dass
,
dass
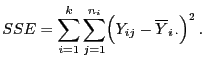 |
(86) |
- Beachte
-
- Wegen der speziellen Gestalt (82) der
Designmatrix
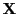 lässt sich die Formel (86)
auch direkt aus der Tatsache herleiten, dass
lässt sich die Formel (86)
auch direkt aus der Tatsache herleiten, dass
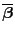 ein KQ-Schätzer ist. Und zwar gilt
ein KQ-Schätzer ist. Und zwar gilt
- Außerdem ergibt sich aus der Bemerkung am Ende von
Abschnitt 3.3.2, dass
wobei
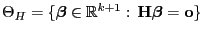 und
und
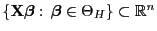 die
Menge derjenigen
die
Menge derjenigen  -dimensionalen Vektoren ist, für die
sämtliche Komponenten gleich sind.
-dimensionalen Vektoren ist, für die
sämtliche Komponenten gleich sind.
- Somit gilt
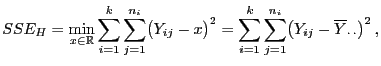 |
(87) |
weil der Mittelwert
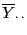 die Quadratsumme
die Quadratsumme
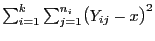 minimiert.
minimiert.
- Hieraus und aus (86) folgt, dass
wobei sich die letzte Gleichheit aus der Quadratsummenzerlegung
ergibt, vgl. die Formel (9) in
Theorem 3.1.
- Für die in Theorem 3.16 betrachtete Testgröße
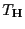 gilt also, dass
gilt also, dass
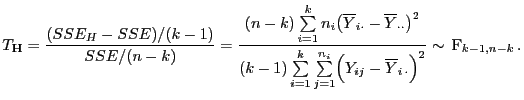 |
(88) |




Nächste Seite: F-Tests für die zweifaktorielle
Aufwärts: Beispiele
Vorherige Seite: Beispiele
Inhalt
Hendrik Schmidt
2006-02-27