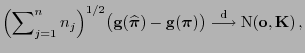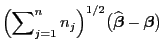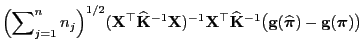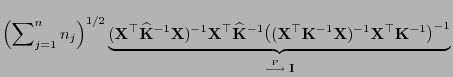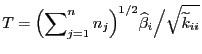Nächste Seite: Bewertung der Anpassungsgüte
Aufwärts: Gewichteter KQ-Schätzer bei kategorialer
Vorherige Seite: Schätzung des Erwartungswertvektors
Inhalt
Asymptotische Normalverteiltheit des KQ-Schätzers
Durch die Gestalt der asymptotischen Kovarianzmatrix
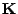 in
Theorem 4.3 wird der folgende Ansatz zur Schätzung
des Parametervektors
in
Theorem 4.3 wird der folgende Ansatz zur Schätzung
des Parametervektors
 motiviert.
motiviert.
- Beachte
-
Wir zeigen nun, dass der gewichtete KQ-Schätzer
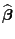 in (62) asymptotisch
normalverteilt ist, wenn die (Teil-) Stichprobenumfänge
in (62) asymptotisch
normalverteilt ist, wenn die (Teil-) Stichprobenumfänge 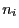 für
jedes
für
jedes
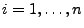 unbegrenzt wachsen.
unbegrenzt wachsen.
Hierfür benötigen wir die folgenden vektoriellen Versionen des
Satzes von Slutsky (vgl. die Theoreme WR-5.9 und WR-5.11) sowie
des ,,Continuous Mapping Theorems'' (vgl. Theorem WR-5.12).
Lemma 4.4
- Sei
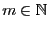 , seien
, seien
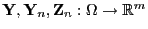 beliebige Zufallsvektoren über einunddemselben
Wahrscheinlichkeitsraum, und sei
beliebige Zufallsvektoren über einunddemselben
Wahrscheinlichkeitsraum, und sei
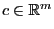 .
.
- Wenn
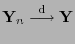 und
und
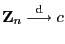 , dann gilt
, dann gilt
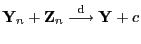 und
und
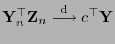 .
.
Lemma 4.5
- Sei
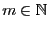 , seien
, seien
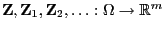 beliebige Zufallsvektoren, und sei
beliebige Zufallsvektoren, und sei
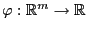 eine
stetige Funktion.
eine
stetige Funktion.
- Dann gilt
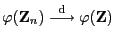 , wenn
, wenn
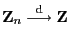 .
.
Die Beweise der Lemmas 4.4 und
4.5 verlaufen ähnlich wie die Beweise der
Theoreme WR-5.9, WR-5.11 bzw. WR-5.12. Sie werden deshalb hier
weggelassen.
Theorem 4.4

Wenn
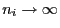
für jedes
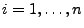
,
so dass
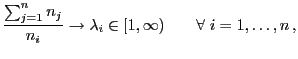 |
(63) |
dann gilt
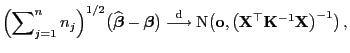 |
(64) |
wobei
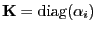
die in
Theorem
betrachtete Diagonalmatrix ist.
- Beweis
-
- Beachte
-




Nächste Seite: Bewertung der Anpassungsgüte
Aufwärts: Gewichteter KQ-Schätzer bei kategorialer
Vorherige Seite: Schätzung des Erwartungswertvektors
Inhalt
Hendrik Schmidt
2006-02-27
![]() in
Theorem 4.3 wird der folgende Ansatz zur Schätzung
des Parametervektors
in
Theorem 4.3 wird der folgende Ansatz zur Schätzung
des Parametervektors
![]() motiviert.
motiviert.
![]() in (62) asymptotisch
normalverteilt ist, wenn die (Teil-) Stichprobenumfänge
in (62) asymptotisch
normalverteilt ist, wenn die (Teil-) Stichprobenumfänge ![]() für
jedes
für
jedes
![]() unbegrenzt wachsen.
unbegrenzt wachsen.