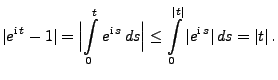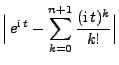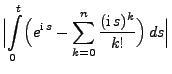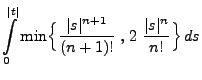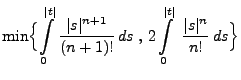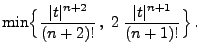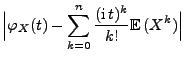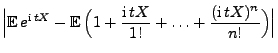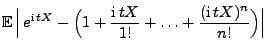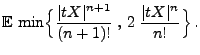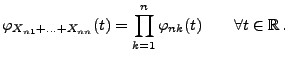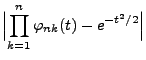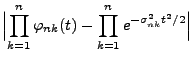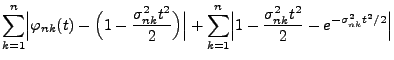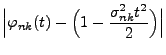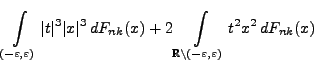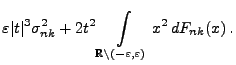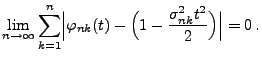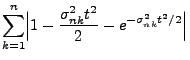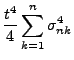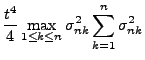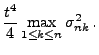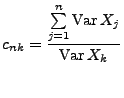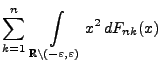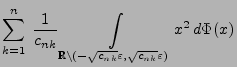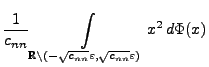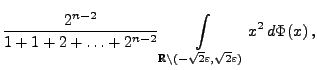Next: Anwendungsbeispiel: Dichteschätzung
Up: Zentraler Grenzwertsatz
Previous: Charakteristische Funktionen
Contents
Bedingungen von Lindeberg und Ljapunow
Der folgende zentrale Grenzwertsatz von Lindeberg kann
sowohl als Verallgemeinerung von Theorem 5.16 als
auch von Lemma 5.9 aufgefasst werden, wenn dabei
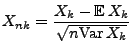 |
(100) |
gesetzt wird.
Theorem 5.22
Für jedes
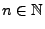
sei
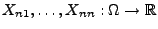
eine
Folge von unabhängigen Zufallsvariablen, die den Bedingungen
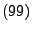
genügen. Falls für jedes
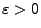
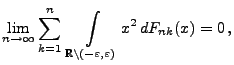 |
(101) |
dann gilt
für jedes
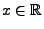
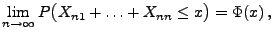 |
(102) |
wobei
![$ \Phi:\mathbb{R}\to[0,1]$](img2046.png)
die Verteilungsfunktion der
Standardnormalverteilung ist.
- Beachte
-
- Beachte
-
- Die Bedingung (101) bedeutet, dass
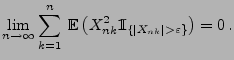 |
(103) |
- Weil
folgt aus (101), dass
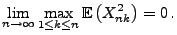 |
(104) |
- Weil
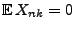 vorausgesetzt wird, ergibt sich aus
(104) und aus der Tschebyschew-Ungleichung
(4.72), dass für jedes
vorausgesetzt wird, ergibt sich aus
(104) und aus der Tschebyschew-Ungleichung
(4.72), dass für jedes
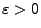
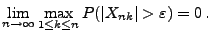 |
(105) |
- Wenn die Bedingung (105) erfüllt ist, dann spricht
man von der (gleichmäßigen) asymptotischen Kleinheit der
Summanden
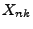 .
.
Im Beweis von Theorem 5.22 benötigen wir die
folgenden Hilfssätze.
Lemma 5.11
Für jedes
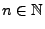
und für beliebige
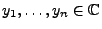
,
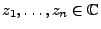
mit
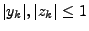
für jedes
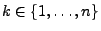
gilt
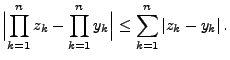 |
(106) |
- Beweis
-
Ähnlich wie in Theorem 5.21 entwickeln wir nun die
charakteristische Funktion 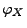 einer Zufallsvariablen
einer Zufallsvariablen  in eine Taylor-Reihe, wobei wir jetzt aber eine andere
Abschätzung des Restgliedes als in (95)
betrachten.
in eine Taylor-Reihe, wobei wir jetzt aber eine andere
Abschätzung des Restgliedes als in (95)
betrachten.
Lemma 5.12
Sei
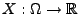
eine beliebige Zufallsvariable mit
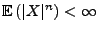
für ein
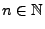
. Dann gilt:
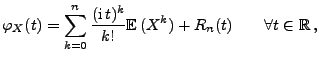 |
(107) |
wobei
- Beweis
-
- Mit vollständiger Induktion zeigen wir zunächst, dass für
beliebige
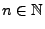 und
und
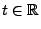
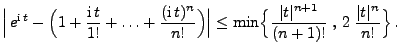 |
(108) |
- Für
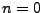 gilt offenbar
und
gilt offenbar
und
- Es gelte nun (108) für ein
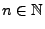 . Dann gilt auch
. Dann gilt auch
- Damit ist die Gültigkeit von (108) für jedes
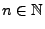 bewiesen.
bewiesen.
- Wenn nun in (108) die Zahl
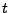 durch
durch 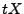 ersetzt
wird und wenn auf beiden Seiten von (108) der
Erwartungswert gebildet wird, dann ergibt sich für jedes
ersetzt
wird und wenn auf beiden Seiten von (108) der
Erwartungswert gebildet wird, dann ergibt sich für jedes
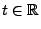
- Damit ist (107) bewiesen.

- Beweis von Theorem 5.22
-
- Für beliebige
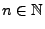 und
und
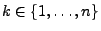 betrachten wir
die charakteristische Funktion
betrachten wir
die charakteristische Funktion
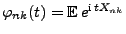 von
von 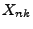 .
.
- Wegen Theorem 5.18 gilt für die charakteristische
Funktion
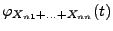 der Summe
der Summe
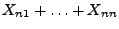
- Wegen des Stetigkeitssatzes für charakteristische Funktionen (vgl.
Theorem 5.20) genügt es also zu zeigen, dass für
jedes
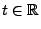
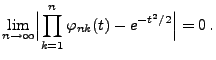 |
(109) |
- Aus (99) und aus Lemma 5.11 ergibt
sich, dass
- Um (109) zu beweisen, genügt es nun zu zeigen, dass
beide Summen in dieser Abschätzung für
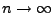 gegen Null
konvergieren.
gegen Null
konvergieren.
- Aus Lemma 5.12 ergibt sich, dass für jedes
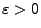
- Weil
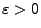 beliebig klein gewählt werden kann, ergibt
sich nun aus (99) und (101), dass
beliebig klein gewählt werden kann, ergibt
sich nun aus (99) und (101), dass
- Um zu zeigen, dass auch die zweite Summe für
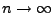 gegen
Null strebt, benutzen wir die Tatsache, dass für
gegen
Null strebt, benutzen wir die Tatsache, dass für
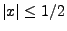 und dass wegen (104)
für jedes hinreichend große
und dass wegen (104)
für jedes hinreichend große 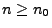 gilt.
gilt.
- Hieraus folgt, dass für
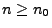
- Aus (104) ergibt sich nun, dass auch die zweite
Summe für
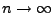 gegen Null strebt.
gegen Null strebt.

Der folgende zentrale Grenzwertsatz von Ljapunow enthält
eine Bedingung, die zwar schärfer, jedoch einfacher handhabbar ist
als die Lindeberg-Bedingung (101) in
Theorem 5.22.
Theorem 5.23
Für jedes
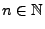
sei
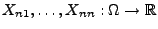
eine
Folge von unabhängigen Zufallsvariablen, die den Bedingungen
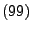
genügen. Falls
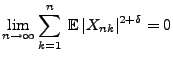 |
(110) |
für ein
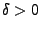
, dann gilt
für jedes
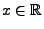
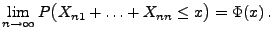 |
(111) |
- Beweis
-
- Für beliebige
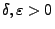 gilt
gilt
- Aus (110) folgt also die Gültigkeit der
Lindeberg-Bedingung (101) in
Theorem 5.22.

- Beachte
-
- In den Theoremen 5.22 bzw. 5.23 haben
wir gezeigt, dass die Lindeberg-Bedingung (101) bzw.
die Ljapunow-Bedingung (110) hinreichend für die
asymptotische Normalverteiltheit der Summe
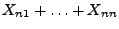 sind.
sind.
- Die Lindeberg-Bedingung (101) und damit auch die
Ljapunow-Bedingung (110) sind im allgemeinen jedoch
nicht notwendig für die asymptotische Normalverteiltheit der
Summe
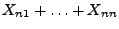
- Wir illustrieren diesen Sachverhalt durch das folgende Beispiel.
- Seien
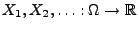 unabhängige normalverteilte
Zufallsvariablen mit
unabhängige normalverteilte
Zufallsvariablen mit
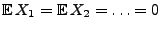 und
und
- Dann ist die Summe
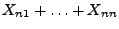 der Zufallsvariablen
der Zufallsvariablen
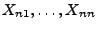 mit
mit
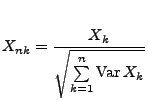 |
(112) |
N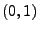 -verteilt wegen der Faltungsstabilität der
Normalverteilung (vgl. Korollar 3.2)).
-verteilt wegen der Faltungsstabilität der
Normalverteilung (vgl. Korollar 3.2)).
- D.h., es gilt insbesondere die asymptotische Normalverteiltheit
(111).
- Die Lindeberg-Bedingung (101) ist jedoch nicht
erfüllt, denn mit der Schreibweise
gilt für die in (112) eingeführten Zufallsvariablen
wobei diese untere Schranke offenbar nicht gegen 0 strebt.
- Der Grund hierfür ist, dass in diesem Beispiel die Summanden
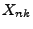 mit großem Index
mit großem Index 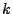 nicht asymptotisch klein im
Sinne von (105) sind, sondern die übrigen Summanden
dominieren.
nicht asymptotisch klein im
Sinne von (105) sind, sondern die übrigen Summanden
dominieren.
Der folgende zentrale Grenzwertsatz, den wir hier ohne Beweis
erwähnen, enthält ein hinreichende und notwendige Bedingung
für die Gültigkeit der asymptotischen Normalverteiltheit
(111).
Theorem 5.24
Für jedes
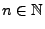
sei
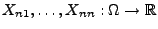
eine
Folge von unabhängigen Zufallsvariablen, die den Bedingungen
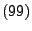
genügen. Es gilt
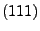
genau
dann, wenn für jedes
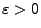
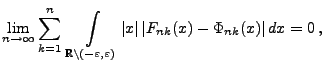 |
(113) |
wobei
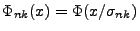
.
Einen Beweis von Theorem 5.24 kann man
beispielsweise in Abschnitt III.4 des Buches A.N. Sirjaev (Wahrscheinlichkeit, Deutscher Verlag der Wissenschaften, Berlin
1988) finden.
- Beachte
 Für das in (112) betrachtete Beispiel
normalverteilter Summanden ist die Bedingung (113)
offenbar erfüllt, denn es gilt
Für das in (112) betrachtete Beispiel
normalverteilter Summanden ist die Bedingung (113)
offenbar erfüllt, denn es gilt
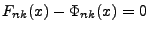 für
jedes
für
jedes
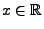 .
.




Next: Anwendungsbeispiel: Dichteschätzung
Up: Zentraler Grenzwertsatz
Previous: Charakteristische Funktionen
Contents
Ursa Pantle
2004-05-10
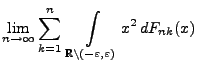
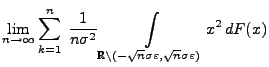
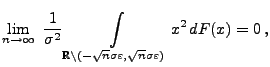
![]() einer Zufallsvariablen
einer Zufallsvariablen ![]() in eine Taylor-Reihe, wobei wir jetzt aber eine andere
Abschätzung des Restgliedes als in (95)
betrachten.
in eine Taylor-Reihe, wobei wir jetzt aber eine andere
Abschätzung des Restgliedes als in (95)
betrachten.