XOR Gate

An XOR gate (symbol \(\dot{\lor}\)) can be represented by the equation

\[A \dot{\lor} B = \bigl(B \barwedge (A \barwedge A)\bigr) \barwedge \bigl(A \barwedge (B \barwedge B)\bigr)\]

Confirm this with a truth table:

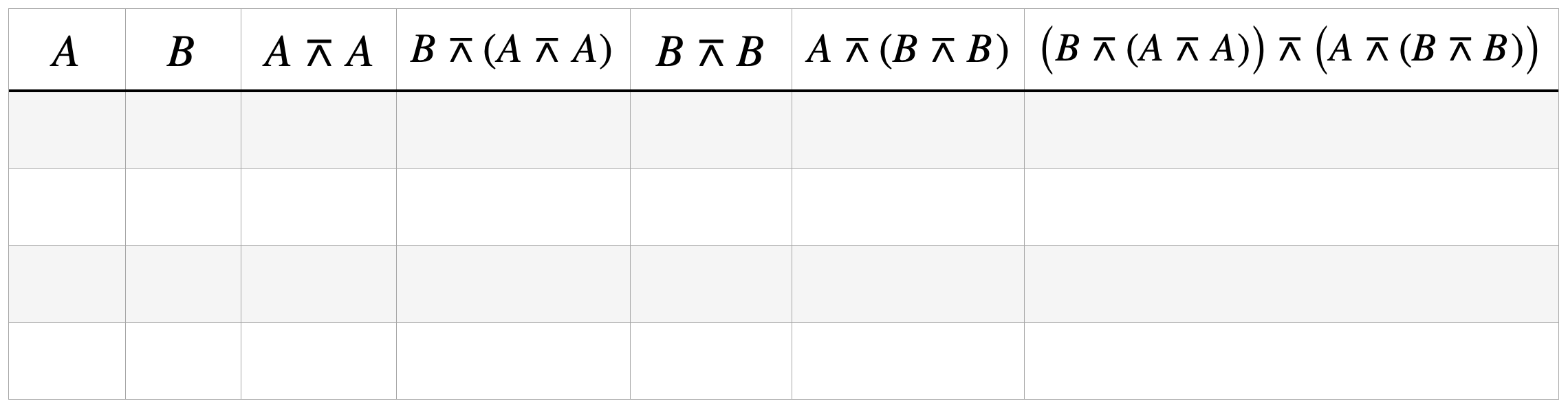
Show with a truth table that also

\[A \dot{\lor} B = \bigl((A \barwedge B) \barwedge A\bigr) \barwedge \bigl((A \barwedge B) \barwedge B \bigr)\]

holds true:

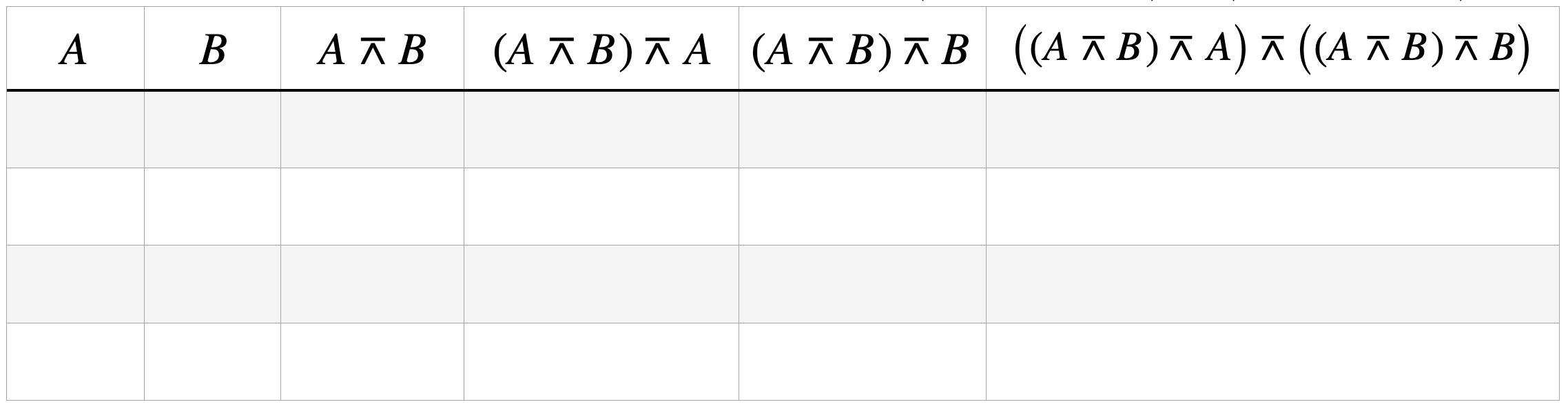
Tasks

Implement both expressions for XOR in CircuitVerse.
Explain to a partner the practical advantage of the second representation.
Additional Challenge: Try to formally transform the first equation into the second equation. You can use to rewrite the logical equation into an algebraic equation.