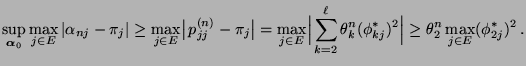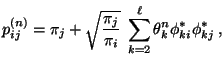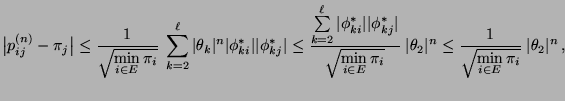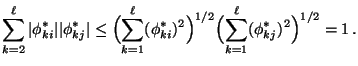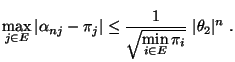Nächste Seite: Multiplikativ reversible Version der
Aufwärts: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Vorherige Seite: Rekursive Konstruktion der ,,Vergangenheit''
Inhalt
Bestimmung der Konvergenzgeschwindigkeit bei Reversibilität
- Sei
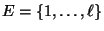 , und sei
, und sei
 eine quasi-positive
(d.h. irreduzible und aperiodische) Übergangsmatrix.
eine quasi-positive
(d.h. irreduzible und aperiodische) Übergangsmatrix.
- Sei also
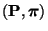 reversibel, wobei
reversibel, wobei
 eine
irreduzible und aperiodische Übergangsmatrix ist.
eine
irreduzible und aperiodische Übergangsmatrix ist.
- Dann ergibt sich aus der Detailed-Balance-Bedingung
(85), dass die Matrix
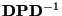 symmetrisch ist, wobei
symmetrisch ist, wobei
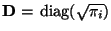 .
.
- Weil die Eigenwerte
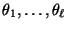 von
von
 mit
den Eigenwerten von
mit
den Eigenwerten von
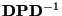 übereinstimmen, gilt
somit
übereinstimmen, gilt
somit
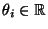 für jedes
für jedes 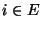 ,
,
- und die rechten Eigenvektoren
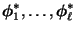 von
von
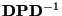 können so gewählt werden, dass ihre
Komponenten reellwertig sind,
können so gewählt werden, dass ihre
Komponenten reellwertig sind,
- dass
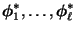 gleichzeitig linke
Eigenvektoren von
gleichzeitig linke
Eigenvektoren von
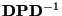 sind und dass sowohl die
Zeilen als auch die Spalten der
sind und dass sowohl die
Zeilen als auch die Spalten der
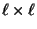 Matrix
Matrix
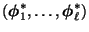 orthonormale Vektoren sind
(vgl. beispielsweise Lemma 3.8 des Vorlesungsskriptes ,,Statistik
II'').
orthonormale Vektoren sind
(vgl. beispielsweise Lemma 3.8 des Vorlesungsskriptes ,,Statistik
II'').
- Aus der Spektraldarstellung (30) von
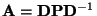 ergibt sich nun, dass für jedes
ergibt sich nun, dass für jedes 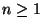
- Hieraus folgt, dass
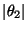 die kleinste positive Zahl ist,
für die die in (96) betrachtete Abschätzung der
Konvergenzgeschwindigkeit gleichmäßig für alle Anfangsverteilungen
die kleinste positive Zahl ist,
für die die in (96) betrachtete Abschätzung der
Konvergenzgeschwindigkeit gleichmäßig für alle Anfangsverteilungen
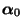 gilt.
gilt.
- Beachte
-
- Aus (97) ergibt sich, dass die
Konvergenzabschätzung (96) wie folgt präzisiert
werden kann. Und zwar gilt
weil die Spaltenvektoren
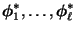 und
damit auch die Zeilenvektoren
und
damit auch die Zeilenvektoren
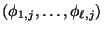 für
für
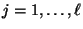 eine orthonormale Basis in
eine orthonormale Basis in
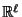 bilden
und sich deshalb aus der Ungleichung von Cauchy-Schwarz ergibt,
dass
bilden
und sich deshalb aus der Ungleichung von Cauchy-Schwarz ergibt,
dass
- Somit gilt
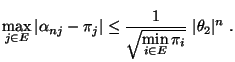 |
(98) |
- Die praktische Nutzbarkeit der Konvergenzabschätzung
(98) kann jedoch aus mehreren Gründen problematisch
sein, weil
- der Vorfaktor in (98) nicht von der Wahl der
Anfangsverteilung
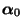 abhängt,
abhängt,
- bei der Herleitung der Konvergenzabschätzung (98)
vorausgesetzt wird, dass die Markov-Kette reversibel ist,
- die Bestimmung des Eigenwertes
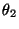 schwierig sein kann,
falls die Anzahl der Zustände
schwierig sein kann,
falls die Anzahl der Zustände 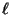 groß ist.
groß ist.
- In Abschnitt 2.3.5 betrachten wir deshalb eine alternative Konvergenzabschätzung,
- deren Vorfaktor von der gewählten Anfangsverteilung abhängt und
- für die nicht vorausgesetzt wird, dass die betrachtete
Markov-Kette reversibel ist,
- und leiten in Abschnitt 2.3.7 eine Schranke für den
zweitgrößten Betrag
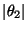 der Eigenwerte von reversiblen
Übergangsmatrizen her.
der Eigenwerte von reversiblen
Übergangsmatrizen her.




Nächste Seite: Multiplikativ reversible Version der
Aufwärts: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Vorherige Seite: Rekursive Konstruktion der ,,Vergangenheit''
Inhalt
Ursa Pantle
2003-09-29
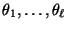 von
von
 voneinander verschieden
sind, hatten wir mit Hilfe des Theorems von Perron-Frobenius
gezeigt (vgl. Korollar 2.4), dass
voneinander verschieden
sind, hatten wir mit Hilfe des Theorems von Perron-Frobenius
gezeigt (vgl. Korollar 2.4), dass
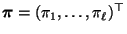 die (eindeutig
bestimmte) Lösung der Gleichung
die (eindeutig
bestimmte) Lösung der Gleichung
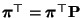 ist.
ist.
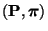 zusätzlich reversibel ist, dann kann man
zeigen, dass die in (96) betrachtete Basis
zusätzlich reversibel ist, dann kann man
zeigen, dass die in (96) betrachtete Basis
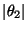 der Konvergenzgeschwindigkeit nicht verbessert
werden kann.
der Konvergenzgeschwindigkeit nicht verbessert
werden kann.
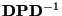 symmetrisch ist, wobei
symmetrisch ist, wobei
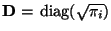 .
.
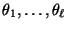 von
von
 mit
den Eigenwerten von
mit
den Eigenwerten von
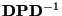 übereinstimmen, gilt
somit
übereinstimmen, gilt
somit
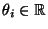 für jedes
für jedes 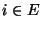 ,
,
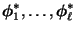 von
von
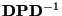 können so gewählt werden, dass ihre
Komponenten reellwertig sind,
können so gewählt werden, dass ihre
Komponenten reellwertig sind,
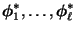 gleichzeitig linke
Eigenvektoren von
gleichzeitig linke
Eigenvektoren von
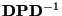 sind und dass sowohl die
Zeilen als auch die Spalten der
sind und dass sowohl die
Zeilen als auch die Spalten der
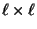 Matrix
Matrix
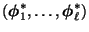 orthonormale Vektoren sind
(vgl. beispielsweise Lemma 3.8 des Vorlesungsskriptes ,,Statistik
II'').
orthonormale Vektoren sind
(vgl. beispielsweise Lemma 3.8 des Vorlesungsskriptes ,,Statistik
II'').
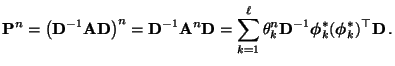
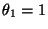 und
und
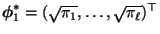 ergibt
sich hieraus, dass für beliebige
ergibt
sich hieraus, dass für beliebige 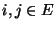
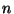 eine gerade Zahl ist bzw. sämtliche Eigenwerte
eine gerade Zahl ist bzw. sämtliche Eigenwerte
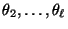 nichtnegativ sind, dann gilt somit
nichtnegativ sind, dann gilt somit