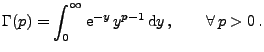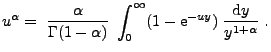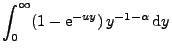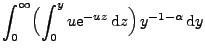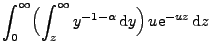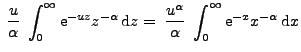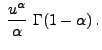Nächste Seite: Martingale
Aufwärts: Lévy-Prozesse
Vorherige Seite: Beispiele: Wiener-Prozess, zusammengesetzte Poisson-Prozesse,
Inhalt
Subordinatoren
Eine weitere Klasse von Lévy-Prozessen, die insbesondere die
zusammengesetzten Poisson-Prozesse mit positiven Sprunghöhen als
Spezialfall umfassen, sind die sogenannten Subordinatoren.
- Definition
 Ein Lévy-Prozess
Ein Lévy-Prozess
 heißt Subordinator,
wenn mit Wahrscheinlichkeit
heißt Subordinator,
wenn mit Wahrscheinlichkeit 
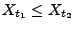 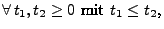 |
(30) |
- wobei sich aus (30) wegen
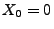 sofort ergibt,
dass
sofort ergibt,
dass 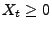 für jedes
für jedes  .
.
Bevor wir einige konkrete Beispiele von Subordinatoren näher
diskutieren, zeigen wir zunächst, wie sich die
Lévy-Chintschin-Darstellung (15) von
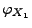 spezifizieren lässt, wenn
spezifizieren lässt, wenn  ein
Subordinator ist.
ein
Subordinator ist.
Theorem 3.5

Der Lévy-Prozess

ist genau dann ein
Subordinator, wenn sich der Lévy-Exponent
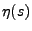
von
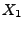
darstellen lässt in der Form
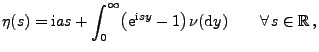 |
(31) |
wobei
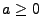
und für das Lévy-Maß
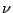
zusätzlich gilt, dass
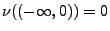 und und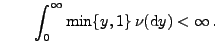 |
(32) |
- Beweis
 Wir zeigen zuerst die Hinlänglichkeit der Bedingungen
(31) und (32).
Wir zeigen zuerst die Hinlänglichkeit der Bedingungen
(31) und (32).
- Falls
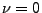 , dann gilt
, dann gilt
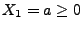 ,
,
- und aus der Stationarität der Zuwächse sowie der stochastischen
Stetigkeit des Lévy-Prozesses
 ergibt sich, dass
ergibt sich, dass
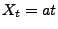 für jedes
für jedes  gilt,
gilt,
- d.h.,
 ist ein Subordinator.
ist ein Subordinator.
- Sei nun
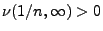 für jedes hinreichend große
für jedes hinreichend große 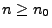 . Aus (31) und (32) ergibt sich
dann, dass für jedes
. Aus (31) und (32) ergibt sich
dann, dass für jedes
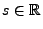
- Für jedes
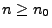 ist dabei
ist dabei
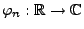 mit
die charakteristische Funktion einer nichtnegativen
Zufallsvariablen
mit
die charakteristische Funktion einer nichtnegativen
Zufallsvariablen 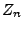 ,
,
- die eine zusammengesetzte Poisson-Verteilung mit den
Charakteristiken
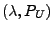 hat
hat
- und zwar mit der ,,Poisson-Intensität''
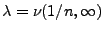 , wobei
, wobei
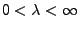 ,
,
- und mit der ,,Sprunghöhen-Verteilung''
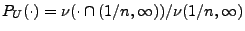 , vgl.
Abschnitt 2.2.2.
, vgl.
Abschnitt 2.2.2.
- Es gilt also
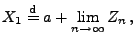 |
(33) |
wobei 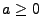 und
und 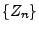 eine Folge von nichtnegativen
Zufallsvariablen ist.
eine Folge von nichtnegativen
Zufallsvariablen ist.
- Aus (33) folgt insbesondere, dass
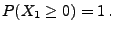 |
(34) |
- Außerdem gilt für jedes
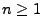 wobei die Zufallsvariablen
wobei die Zufallsvariablen
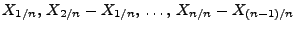 unabhängig und identisch verteilt sind.
unabhängig und identisch verteilt sind.
- Hieraus und aus (34) folgt, dass mit
Wahrscheinlichkeit

- Aus der Stationarität der Zuwächse des Lévy-Prozesses
 ergibt sich nun, dass
bzw.
ergibt sich nun, dass
bzw.
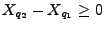  |
(35) |
- Für
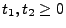 mit
mit 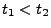 seien
seien
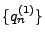 und
und
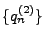 zwei Folgen rationaler Zahlen, so dass
zwei Folgen rationaler Zahlen, so dass
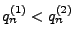 für jedes
für jedes 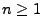 und
und
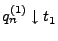 bzw.
bzw.
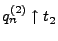 .
.
- Dann ergibt sich aus (35), dass für jedes
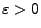
- wobei sich der letzte Grenzwert aus der Tatsache ergibt, dass
wegen der stochastischen Stetigkeit von

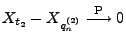
und
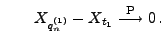
- Damit ist gezeigt, dass
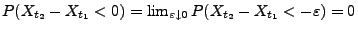 bzw.
bzw.
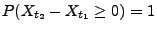 , d.h.,
, d.h.,  ist ein Subordinator.
ist ein Subordinator.
Die Notwendigkeit der Bedingungen (31) und
(32) kann man sich wie folgt überlegen.
- Beachte
-
Außer den zusammengesetzten Poisson-Prozessen mit positiven
Sprunghöhen, die wir bereits am Anfang dieses Abschnittes erwähnt
haben und deren Lévy-Maß 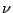 endlich ist, gibt es noch weitere
Klassen von Subordinatoren (mit unendlichem Lévy-Maß).
endlich ist, gibt es noch weitere
Klassen von Subordinatoren (mit unendlichem Lévy-Maß).
- Beispiel
- (
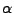 -stabile Subordinatoren)
-stabile Subordinatoren)
- Sei
 ein Subordinator mit
ein Subordinator mit 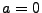 , dessen
Lévy-Maß
, dessen
Lévy-Maß 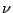 gegeben ist durch
gegeben ist durch
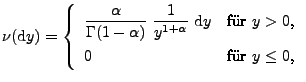 |
(40) |
wobei
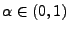 und
und
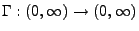 die
Gammafunktion bezeichnet mit
die
Gammafunktion bezeichnet mit
- Beachte: Das in (40) gegebene Lévy-Maß
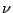 hat
die Form (29).
hat
die Form (29).
- Außerdem kann man in diesem Fall
leicht zeigen, dass (28) gilt bzw. (äquivalent
hierzu) dass
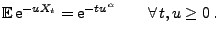 |
(41) |




Nächste Seite: Martingale
Aufwärts: Lévy-Prozesse
Vorherige Seite: Beispiele: Wiener-Prozess, zusammengesetzte Poisson-Prozesse,
Inhalt
Ursa Pantle
2005-07-13
![]() spezifizieren lässt, wenn
spezifizieren lässt, wenn ![]() ein
Subordinator ist.
ein
Subordinator ist.
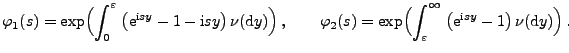
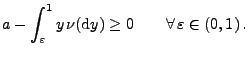
![]() endlich ist, gibt es noch weitere
Klassen von Subordinatoren (mit unendlichem Lévy-Maß).
endlich ist, gibt es noch weitere
Klassen von Subordinatoren (mit unendlichem Lévy-Maß).