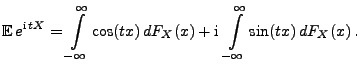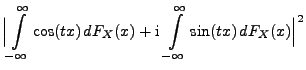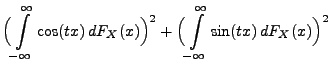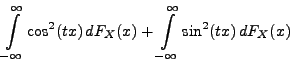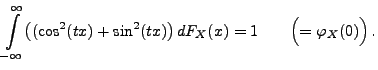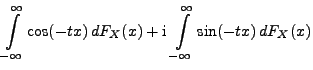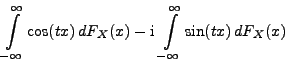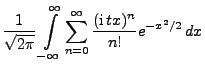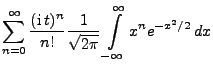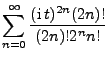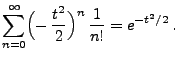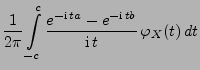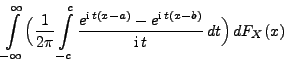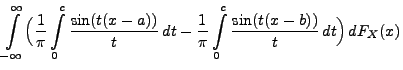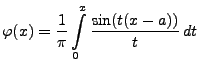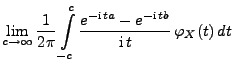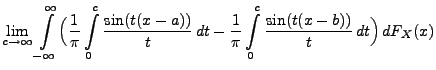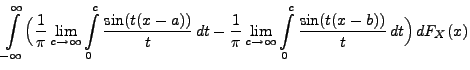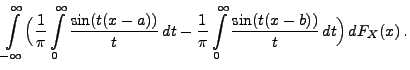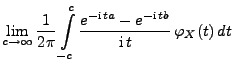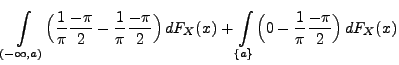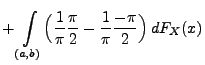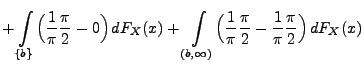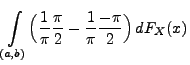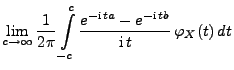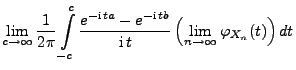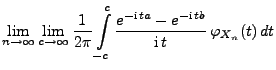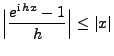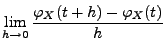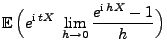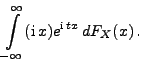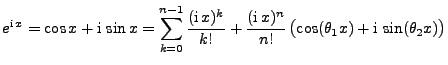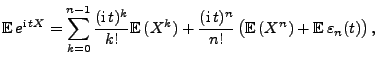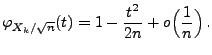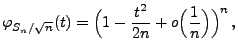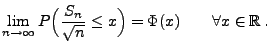Next: Bedingungen von Lindeberg und
Up: Zentraler Grenzwertsatz
Previous: Anwendungsbeispiele
Contents
Charakteristische Funktionen
Charakteristische Funktionen sind ein wichtiges analytisches
Hilfsmittel in der Stochastik, insbesondere bei der Herleitung des
zentralen Grenzwertsatzes für Summen von unabhängigen, jedoch
nichtnotwendig identisch verteilten Zufallsvariablen; vgl. die
Abschnitte 5.3.4 und 5.3.5.
- Definition
 Sei
Sei
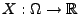 eine beliebige
Zufallsvariable. Die charakteristische Funktion
eine beliebige
Zufallsvariable. Die charakteristische Funktion
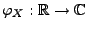 von
von  ist dann gegeben durch
ist dann gegeben durch
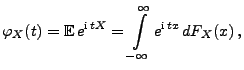 |
(78) |
wobei das Integral als Lebesgue-Stieltjes-Integral aufgefasst
wird.
- Beachte
-
Wir zeigen zunächst einige elementare Eigenschaften von
charakteristischen Funktionen.
Theorem 5.17
Sei
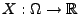
eine beliebige Zufallsvariable, und seien
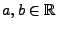
beliebige reelle Zahlen. Dann gilt:
- 1.
- Für jedes
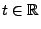 ist
ist
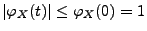 |
(79) |
und
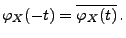 |
(80) |
- 2.
- Die charakteristische Funktion
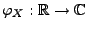 ist
gleichmäßig stetig.
ist
gleichmäßig stetig.
- 3.
- Für die charakteristische
Funktion
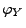 von
von 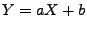 gilt
gilt
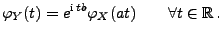 |
(81) |
- Beweis
-
- Die Gültigkeit von (79) ergibt sich aus der
Jensen-Ungleichung (4.71), denn für jedes
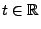 gilt
gilt
- Die Gleichung (80) ergibt sich auf ähnliche Weise,
denn es gilt für jedes
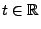
- Außerdem gilt für beliebige
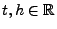
- Hieraus ergibt sich die gleichmäßige Stetigkeit von
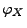 ,
weil wegen des Satzes von Lebesgue über die beschränkte Konvergenz
,
weil wegen des Satzes von Lebesgue über die beschränkte Konvergenz
- Für die charakteristische Funktion
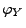 von
von 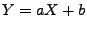 gilt
gilt

- Beispiel
-
Wir leiten nun eine einfache Formel für die charakteristische
Funktion von Summen von unabhängigen Zufallsvariablen her.
Theorem 5.18
Seien
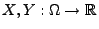
unabhängige Zufallsvariablen. Dann gilt
für jedes
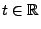
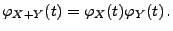 |
(86) |
- Beweis
 Weil
Weil  und
und 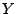 unabhängig sind, sind wegen
Theorem 3.18 auch die Zufallsvariablen
unabhängig sind, sind wegen
Theorem 3.18 auch die Zufallsvariablen 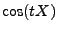 und
und 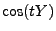 ,
, 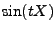 und
und 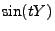 bzw.
bzw.
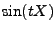 und
und 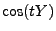 jeweils
unabhängig, und für jedes
jeweils
unabhängig, und für jedes
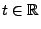 gilt somit
gilt somit

In Theorem 5.19 beweisen wir eine nützliche Umkehrformel für charakteristische Funktionen. Hierfür benötigen
wir die folgende trigonometrische Identität.
Einen Beweis von Lemma 5.10 kann man
beispielsweise in dem Buch von K.L. Chung (A Course in
Probability Theory, Academic Press, New York 1974) finden.
Theorem 5.19
Sei
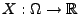
eine beliebige Zufallsvariable mit der
Verteilungsfunktion
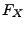
. Für beliebige Stetigkeitspunkte
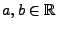
von
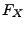
mit
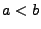
gilt
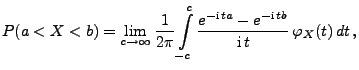 |
(88) |
wobei
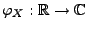
die charakteristische Funktion von

ist.
- Beweis
-
- Beachte
-
- Aus Theorem 5.19 ergibt sich der folgende Eindeutigkeitssatz für charakteristische Funktionen.
- D.h., die Verteilung
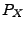 einer Zufallsvariablen
einer Zufallsvariablen  ist
eindeutig durch die charakteristische Funktion
ist
eindeutig durch die charakteristische Funktion 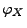 von
von  bestimmt.
bestimmt.
Korollar 5.5
Seien
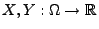
beliebige Zufallsvariablen. Dann gilt
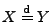
, falls
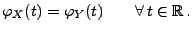 |
(89) |
- Beweis
-
Aus Theorem 5.19 ergibt sich schließlich der folgende
Stetigkeitssatz für charakteristische Funktionen.
Theorem 5.20
Seien
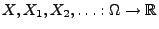
beliebige Zufallsvariablen.
Es gilt
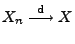
genau dann, wenn
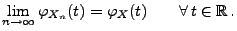 |
(91) |
- Beweis
-
Wir betrachten nun noch den Zusammenhang zwischen den Momenten und
der charakteristischen Funktion von Zufallsvariablen. Dabei zeigen
wir, wie die charakteristische Funktion in eine Taylor-Reihe
entwickelt werden kann.
Theorem 5.21
Sei
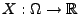
eine beliebige Zufallsvariable mit der
Verteilungsfunktion
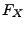
. Falls
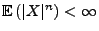
für ein
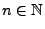
, dann gilt:
- 1.
- Die charakteristische Funktion
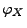 von
von  ist
ist  -mal
stetig differenzierbar, und
-mal
stetig differenzierbar, und
- 2.
- für jedes
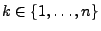
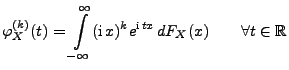 |
(93) |
bzw.
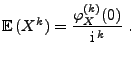 |
(94) |
- 3.
- Außerdem gilt die Taylor-Reihenentwicklung
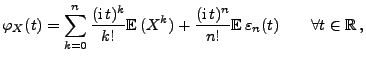 |
(95) |
wobei
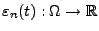 eine Zufallsvariable ist mit
eine Zufallsvariable ist mit
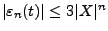 für jedes
für jedes
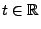 und
und
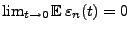 .
.
- Beweis
-
- Beachte
-
- Mit Hilfe der Eigenschaften charakteristischer Funktionen, die in
den Theoremen 5.18, 5.20 und
5.21 bewiesen wurden, kann nun der zentrale
Grenzwertsatz in Theorem 5.16 für Summen von
unabhängigen und identisch verteilten Zufallsvariablen ohne
weiteres hergeleitet werden.
- Zur Erinnerung: In Theorem 5.16 hatten wir
gezeigt, dass für jede Folge
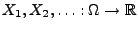 von unabhängigen und identisch verteilten
Zufallsvariablen mit
von unabhängigen und identisch verteilten
Zufallsvariablen mit
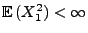 und
und
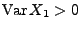 gilt:
gilt:
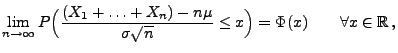 |
(98) |
wobei
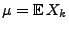 und
und
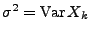 für jedes
für jedes
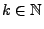 .
.
- Weil
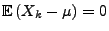 und
und
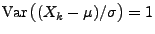 können wir o.B.d.A. beim Beweis von Theorem 5.16
voraussetzen, dass
können wir o.B.d.A. beim Beweis von Theorem 5.16
voraussetzen, dass
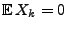 und
und
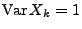 , indem wir die
Gültigkeit von Theorem 5.16 zunächst für die
(unabhängigen und identisch verteilten) Zufallsvariablen
, indem wir die
Gültigkeit von Theorem 5.16 zunächst für die
(unabhängigen und identisch verteilten) Zufallsvariablen
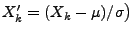 zeigen.
zeigen.
- Sei also
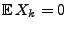
und
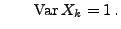
- Aus Theorem 5.21 ergibt sich dann, dass für beliebige
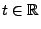 und
und
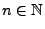
- Aus Theorem 5.18 ergibt sich nun, dass für
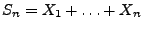 wobei
wobei
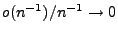 für
für
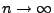 . Hieraus folgt,
dass
. Hieraus folgt,
dass
- Aus Theorem 5.20 ergibt sich somit, dass





Next: Bedingungen von Lindeberg und
Up: Zentraler Grenzwertsatz
Previous: Anwendungsbeispiele
Contents
Ursa Pantle
2004-05-10