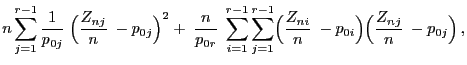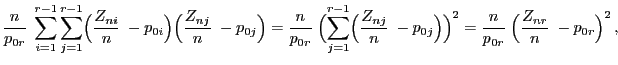Nächste Seite: Güteeigenschaften; lokale Alternativen
Aufwärts: -Anpassungstest
Vorherige Seite: Klassenbildung; Pearson-Statistik
Inhalt
Asymptotische Verteilung
Wir zeigen, dass
 in Verteilung gegen die
in Verteilung gegen die
 -Verteilung mit
-Verteilung mit  Freiheitsgraden strebt, wenn
Freiheitsgraden strebt, wenn
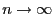 . Dies ist die Grundlage des
. Dies ist die Grundlage des  -Anpassungstests, der von Karl Pearson (1857-1936) eingeführt
worden ist.
-Anpassungstests, der von Karl Pearson (1857-1936) eingeführt
worden ist.
Theorem 5.5
Für jedes
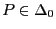
gilt
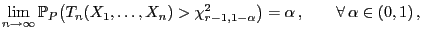 |
(37) |
wobei
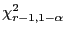
das
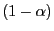
-Quantil der

-Verteilung mit
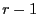
Freiheitsgraden bezeichnet.
- Beweis
-
- In Lemma 5.4 hatten wir gezeigt, dass der in
(32) gegebene Zufallsvektor
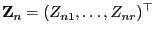 , wobei
, wobei
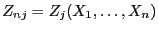 , multinomialverteilt ist unter
, multinomialverteilt ist unter
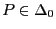 mit den Parametern
mit den Parametern
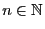 und
und
![$\displaystyle {\mathbf{p}}_0=(p_{01},\ldots,p_{0,r-1})^\top\in[0,1]^{r-1} ,$](img2037.png)
wobei
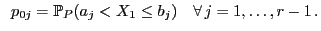
- Mit der Schreibweise
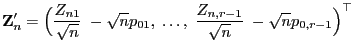 |
(39) |
ergibt sich somit aus Lemma 5.2, dass für
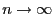
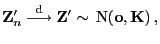 |
(40) |
- Man kann sich leicht überlegen, dass
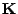 invertierbar ist,
wobei die Eintragungen
invertierbar ist,
wobei die Eintragungen 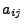 der inversen Matrix
der inversen Matrix
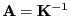 gegeben sind durch
gegeben sind durch
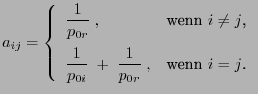 |
(42) |
- Aus (40) und aus den Eigenschaften von
Lineartransformationen normalverteilter Zufallsvektoren (vgl.
Theorem 1.3) ergibt sich nun mit Hilfe von
Lemma 4.5, dass
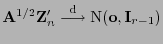 , wobei
, wobei
 die
die
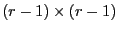 -dimensionale Einheitsmatrix ist.
-dimensionale Einheitsmatrix ist.
- Die erneute Anwendung von Lemma 4.5 ergibt somit,
dass
- Es genügt nun zu beachten, dass
- Es gilt nämlich
- wobei sich der zweite Summand des letzten Ausdruckes schreiben
lässt in der Form
- denn offenbar gilt
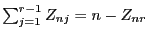 und
und
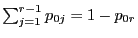 .
.

- Beachte
-
- Bei der praktischen Durchführung des
 -Anpassungstests zur Prüfung der Hypothese
-Anpassungstests zur Prüfung der Hypothese
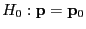 ist
zunächst der Wert der in (36) definierten Testgröße
ist
zunächst der Wert der in (36) definierten Testgröße
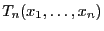 zu berechnen.
zu berechnen.
- Eine ,,Faustregel'' dafür, dass
 hinreichend groß ist, ist die
Gültigkeit der Ungleichung
hinreichend groß ist, ist die
Gültigkeit der Ungleichung
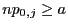 für jedes
für jedes
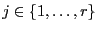 und für eine Konstante
und für eine Konstante 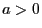 .
.
- Über die erforderliche Größe von
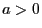 gibt es unterschiedliche
Auffassungen in der Literatur, die von
gibt es unterschiedliche
Auffassungen in der Literatur, die von 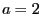 bis
bis 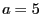 reichen.
Manche Autoren fordern sogar, dass
reichen.
Manche Autoren fordern sogar, dass 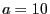 .
.
- Andere Autoren meinen, dass bei einer großen Zahl von Klassen
(etwa
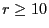 ) auch schon für
) auch schon für 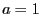 die Approximation
hinreichend gut ist.
die Approximation
hinreichend gut ist.




Nächste Seite: Güteeigenschaften; lokale Alternativen
Aufwärts: -Anpassungstest
Vorherige Seite: Klassenbildung; Pearson-Statistik
Inhalt
Hendrik Schmidt
2006-02-27
![]() in Verteilung gegen die
in Verteilung gegen die
![]() -Verteilung mit
-Verteilung mit ![]() Freiheitsgraden strebt, wenn
Freiheitsgraden strebt, wenn
![]() . Dies ist die Grundlage des
. Dies ist die Grundlage des ![]() -Anpassungstests, der von Karl Pearson (1857-1936) eingeführt
worden ist.
-Anpassungstests, der von Karl Pearson (1857-1936) eingeführt
worden ist.