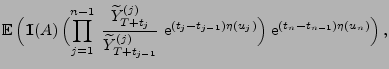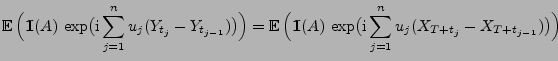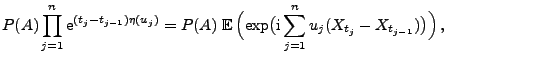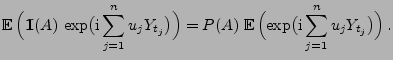Nächste Seite: Reflexionsprinzip des Wiener-Prozesses; Verteilung
Aufwärts: Anwendungsbeispiele
Vorherige Seite: Anwendungsbeispiele
Inhalt
Regeneration von Lévy-Prozessen zu Stoppzeiten
In Theorem 2.23 hatten wir für Fall, dass
 ein (Standard-) Wiener-Prozess ist, ein
Schranke für die Tailfunktion von
ein (Standard-) Wiener-Prozess ist, ein
Schranke für die Tailfunktion von
![$ \max_{t\in[0,1]}
X_t$](img1150.png) hergeleitet.
hergeleitet.
Im nachfolgenden Abschnitt 3.3.2 werden wir zeigen,
dass diese Schranke ,,optimal'' ist, d.h. mit der Tailfunktion von
![$ \max_{t\in[0,1]}
X_t$](img1150.png) übereinstimmt. Hierfür zeigen wir zunächst,
dass Lévy-Prozesse zu endlichen Stoppzeiten die folgende Regenerationseigenschaft
besitzen.
übereinstimmt. Hierfür zeigen wir zunächst,
dass Lévy-Prozesse zu endlichen Stoppzeiten die folgende Regenerationseigenschaft
besitzen.
Theorem 3.14
- Sei
 ein Lévy-Prozess über
ein Lévy-Prozess über
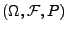 und sei
und sei
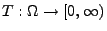 eine endliche Stoppzeit bezüglich
der natürlichen Filtration
eine endliche Stoppzeit bezüglich
der natürlichen Filtration
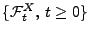 von
von  .
.
- Dann ist der Prozess
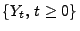 mit
mit
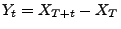 ebenfalls ein Lévy-Prozess, der adaptiert ist bezüglich der
Filtration
ebenfalls ein Lévy-Prozess, der adaptiert ist bezüglich der
Filtration
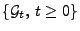 mit
mit
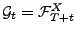 ,
wobei
,
wobei
- der Lévy-Prozess
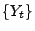 unabhängig von
unabhängig von
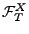 ist und
ist und
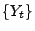 die gleiche Lévy-Charakteristik wie
die gleiche Lévy-Charakteristik wie  hat.
hat.
- Beweis





Nächste Seite: Reflexionsprinzip des Wiener-Prozesses; Verteilung
Aufwärts: Anwendungsbeispiele
Vorherige Seite: Anwendungsbeispiele
Inhalt
Ursa Pantle
2005-07-13
![]() ein (Standard-) Wiener-Prozess ist, ein
Schranke für die Tailfunktion von
ein (Standard-) Wiener-Prozess ist, ein
Schranke für die Tailfunktion von
![]() hergeleitet.
hergeleitet.
![]() übereinstimmt. Hierfür zeigen wir zunächst,
dass Lévy-Prozesse zu endlichen Stoppzeiten die folgende Regenerationseigenschaft
besitzen.
übereinstimmt. Hierfür zeigen wir zunächst,
dass Lévy-Prozesse zu endlichen Stoppzeiten die folgende Regenerationseigenschaft
besitzen.