Nächste Seite: Wiener-Prozesse mit negativer Drift
Aufwärts: Anwendungsbeispiele
Vorherige Seite: Regeneration von Lévy-Prozessen zu
Inhalt
Reflexionsprinzip des Wiener-Prozesses;
Verteilung des Maximums
Mit Hilfe von Theorem 3.14 leiten wir nun das
folgende Reflexionsprinzip des Wiener-Prozesses her. Es
betrifft eine weitere Invarianzeigenschaft des Wiener-Prozesses
(zusätzlich zu den bereits in Theorem 2.24
hergeleiteten Eigenschaften dieses Typs).
- Beweis

- Beachte
-
- Sei
 ein Wiener-Prozess. Die natürliche
Filtration
ein Wiener-Prozess. Die natürliche
Filtration
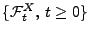 von
von  ist dann gemäß
Theorem 3.13 rechtsstetig.
ist dann gemäß
Theorem 3.13 rechtsstetig.
- Aus Theorem 3.6 folgt somit, dass für jedes
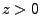 die Ersterreichungszeit
die Ersterreichungszeit
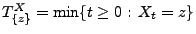 eine
Stoppzeit bezüglich
eine
Stoppzeit bezüglich
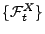 ist.
ist.
- Außerdem ergibt sich aus Korollar 2.5, dass
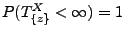 , d.h.,
, d.h.,
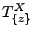 ist eine endliche
Stoppzeit.
ist eine endliche
Stoppzeit.
Die Anwendung von Theorem 3.15 auf die
Ersterreichungszeit
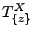 führt nun zu der folgenden
Identität.
führt nun zu der folgenden
Identität.
Korollar 3.5

Sei

ein Wiener-Prozess und sei
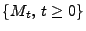
der Maximum-Prozess mit
![$\displaystyle M_t=\max_{s\in[0,t]}X_s\qquad\forall\,t\ge 0\,.$](img1933.png) |
(7) |
Dann gilt für beliebige
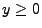
und
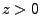
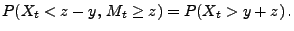 |
(8) |
- Beweis

- Die in (7) betrachtete Abbildung
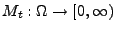 ist eine wohldefinierte Zufallsvariable,
weil die Trajektorien von
ist eine wohldefinierte Zufallsvariable,
weil die Trajektorien von  stetige Funktionen sind, vgl.
auch die Formel (24) in
Abschnitt 2.4.5.
stetige Funktionen sind, vgl.
auch die Formel (24) in
Abschnitt 2.4.5.
- Für die endliche Stoppzeit
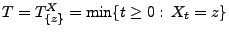 ergibt sich dann aus Theorem 3.15, dass
ergibt sich dann aus Theorem 3.15, dass
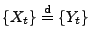
bzw.
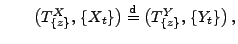
- wobei
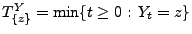 die
Ersterreichungszeit des Niveaus
die
Ersterreichungszeit des Niveaus  durch den in
(5) eingeführten Wiener-Prozess
durch den in
(5) eingeführten Wiener-Prozess 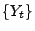 ist.
ist.
- Hieraus folgt, dass
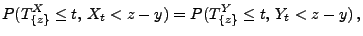 |
(9) |
- Weil außerdem
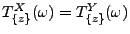 für jedes
für jedes
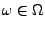 , ergibt sich aus (5), dass
, ergibt sich aus (5), dass
- Hieraus und aus (9) folgt nun, dass
- Damit ist die Behauptung (8) beweisen, weil
offenbar
und

Mit Hilfe von Korollar 3.5 können wir nun zeigen,
dass die in Theorem 2.23 hergeleitete Schranke für
die Tailfunktion von
![$ M_t=\max_{s\in[0,t]} X_s$](img1948.png) ,,optimal'' ist, d.h. mit der Tailfunktion von
,,optimal'' ist, d.h. mit der Tailfunktion von 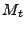 übereinstimmt.
übereinstimmt.
Theorem 3.16

Sei
![$ \{X_t,\,t\in [0,1]\}$](img72.png)
ein Wiener-Prozess. Dann gilt für
beliebige
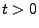
und
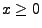
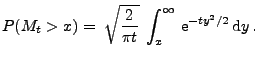 |
(10) |
- Beweis
-




Nächste Seite: Wiener-Prozesse mit negativer Drift
Aufwärts: Anwendungsbeispiele
Vorherige Seite: Regeneration von Lévy-Prozessen zu
Inhalt
Ursa Pantle
2005-07-13
 ein (Standard-) Wiener-Prozess über
ein (Standard-) Wiener-Prozess über
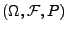 und sei
und sei
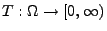 eine endliche
Stoppzeit bezüglich der natürlichen Filtration
eine endliche
Stoppzeit bezüglich der natürlichen Filtration
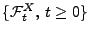 von
von  .
.
 die gleiche Verteilung wie der ,,reflektierte
Prozess''
die gleiche Verteilung wie der ,,reflektierte
Prozess''
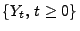 mit
mit
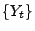 ist ebenfalls ein (Standard-) Wiener-Prozess.
ist ebenfalls ein (Standard-) Wiener-Prozess.