



Nächste Seite: Subordinatoren als Prozesse von
Aufwärts: Anwendungsbeispiele
Vorherige Seite: Reflexionsprinzip des Wiener-Prozesses; Verteilung
Inhalt
Wiener-Prozesse mit negativer Drift
Sei
 ein (Standard-) Wiener-Prozess und für
ein (Standard-) Wiener-Prozess und für
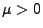 sei
sei
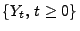 mit
mit
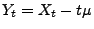 ein
Wiener-Prozess mit negativer Drift.
ein
Wiener-Prozess mit negativer Drift.
Wir beweisen nun eine Formel für die Tailfunktion des Supremums
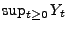 , wobei
, wobei
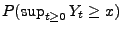 für jedes
für jedes
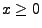 als ,,Ruinwahrscheinlichkeit'' über dem unendlichen
Zeithorizont
als ,,Ruinwahrscheinlichkeit'' über dem unendlichen
Zeithorizont
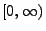 aufgefasst werden kann.
aufgefasst werden kann.
Dabei zeigen wir insbesondere, dass die Schranke für
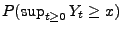 ,,exakt'' ist, die wir bereits in Formel
(19) des Abschnittes 3.2.4 hergeleitet
hatten.
,,exakt'' ist, die wir bereits in Formel
(19) des Abschnittes 3.2.4 hergeleitet
hatten.
Theorem 3.17

Sei

ein
Wiener-Prozess. Dann gilt für beliebige
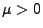
und
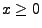
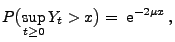 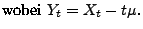 |
(11) |
- Beweis

- Für beliebige
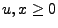 betrachten wir das Martingal
betrachten wir das Martingal
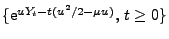 und die (endliche) Stoppzeit
und die (endliche) Stoppzeit
- Aus Korollar 3.4 ergibt sich dann, dass für
beliebige
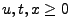 bzw.
bzw.
![$\displaystyle {\mathbb{E}\,}\bigl[\,\exp\bigl(u x-T_{\{x\}}(u^2/2-\mu u)\bigr);...
...{E}\,}\bigl[\,\exp\bigl(u Y_t-t(u^2/2-\mu u)\bigr);\,T_{\{x\}}\ge t\bigr] =1\,.$](img1968.png) |
(12) |
- Weil aus Korollar 2.4 folgt, dass
 mit Wahrscheinlichkeit
mit Wahrscheinlichkeit  , gilt für jedes
, gilt für jedes 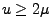 mit Wahrscheinlichkeit
mit Wahrscheinlichkeit  .
.
- Außerdem gilt
wobei der letzte Ausdruck eine (bezüglich
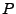 ) integrierbare
Majorante ist.
) integrierbare
Majorante ist.
- Aus dem Satz von Lebesgue über die majorisierte Konvergenz folgt
also, dass für jedes
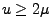
- Hieraus und aus (12) ergibt sich nun, dass
- Insbesondere ergibt sich für
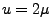 , dass für jedes
, dass für jedes 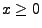
- Damit gilt auch
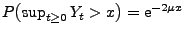 für jedes
für jedes 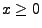 .
.





Nächste Seite: Subordinatoren als Prozesse von
Aufwärts: Anwendungsbeispiele
Vorherige Seite: Reflexionsprinzip des Wiener-Prozesses; Verteilung
Inhalt
Ursa Pantle
2005-07-13
![]() ein (Standard-) Wiener-Prozess und für
ein (Standard-) Wiener-Prozess und für
![]() sei
sei
![]() mit
mit
![]() ein
Wiener-Prozess mit negativer Drift.
ein
Wiener-Prozess mit negativer Drift.
![]() , wobei
, wobei
![]() für jedes
für jedes
![]() als ,,Ruinwahrscheinlichkeit'' über dem unendlichen
Zeithorizont
als ,,Ruinwahrscheinlichkeit'' über dem unendlichen
Zeithorizont
![]() aufgefasst werden kann.
aufgefasst werden kann.
![]() ,,exakt'' ist, die wir bereits in Formel
(19) des Abschnittes 3.2.4 hergeleitet
hatten.
,,exakt'' ist, die wir bereits in Formel
(19) des Abschnittes 3.2.4 hergeleitet
hatten.