



Nächste Seite: Stochastische Prozesse und Felder
Aufwärts: Anwendungsbeispiele
Vorherige Seite: Wiener-Prozesse mit negativer Drift
Inhalt
Subordinatoren als Prozesse von Ersterreichungszeiten
In diesem Abschnitt diskutieren wir zwei weitere Beispiele, bei
dem Theorem 3.15 auf die Ersterreichungszeit
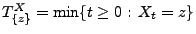 des (Standard-)
Wiener-Prozesses
des (Standard-)
Wiener-Prozesses
 angewendet wird;
angewendet wird; 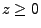 .
.
Zur Erinnerung: Ein Subordinator
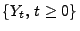 heißt
heißt
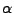 -stabiler Lévy-Prozess mit Stabilitätsindex
-stabiler Lévy-Prozess mit Stabilitätsindex
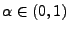 , wenn
, wenn 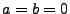 und das Lévy-Maß
und das Lévy-Maß 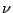 gegeben ist
durch
gegeben ist
durch
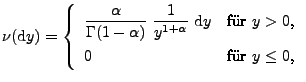 |
(13) |
wobei
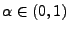 und
und
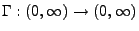 die
Gammafunktion bezeichnet mit
die
Gammafunktion bezeichnet mit
- Beachte
-
Theorem 3.18

Sei

ein
Wiener-Prozess. Dann ist der Prozess der Ersterreichungszeiten
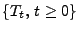
mit
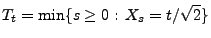 |
(15) |
ein Lévy-Prozess, der die gleiche Verteilung wie der
Lévy-Subordinator hat.
- Beweis

Wir verallgemeinern nun das Modell von Theorem 3.18
und betrachten Prozesse von Ersterreichungszeiten für
Wiener-Prozesse mit Drift.
Theorem 3.19

Sei

ein
Wiener-Prozess. Für beliebige
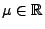
und
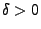
ist dann
der Prozess der Ersterreichungszeiten
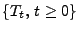
mit
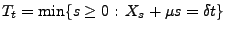 |
(17) |
ein Lévy-Prozess, wobei
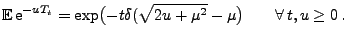 |
(18) |
Der Beweis von Theorem 3.19 verläuft ähnlich
wie der Beweis von Theorem 3.18. Er wird deshalb
weggelassen.
- Beachte
-
- Für die in Theorem 3.19 betrachteten
Ersterreichungszeiten
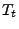 mit der in (18)
gegebenen Laplace-Transformierten kann man zeigen, dass für jedes
mit der in (18)
gegebenen Laplace-Transformierten kann man zeigen, dass für jedes
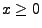
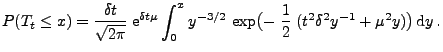 |
(19) |
- Man sagt, dass Zufallsvariablen mit der in (19)
gegebenen Verteilungsfunktion eine inverse Gauß-Verteilung
besitzen.
Die in den Theoremen 3.18 bzw. 3.19
betrachteten Subordinatoren
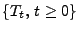 spielen eine
wichtige Rolle bei der Zeitransformation von
Lévy-Prozessen.
spielen eine
wichtige Rolle bei der Zeitransformation von
Lévy-Prozessen.
Es gilt nämlich die folgende Invarianz-Eigenschaft von
Lévy-Prozessen, die wir hier ohne Beweis angeben.
Ein Beweis von Theorem 3.20 kann zum Beispiel
in Applebaum (2004), S. 53-55 nachgelesen werden.




Nächste Seite: Stochastische Prozesse und Felder
Aufwärts: Anwendungsbeispiele
Vorherige Seite: Wiener-Prozesse mit negativer Drift
Inhalt
Ursa Pantle
2005-07-13
![]() des (Standard-)
Wiener-Prozesses
des (Standard-)
Wiener-Prozesses
![]() angewendet wird;
angewendet wird; ![]() .
.
![]() heißt
heißt
![]() -stabiler Lévy-Prozess mit Stabilitätsindex
-stabiler Lévy-Prozess mit Stabilitätsindex
![]() , wenn
, wenn ![]() und das Lévy-Maß
und das Lévy-Maß ![]() gegeben ist
durch
gegeben ist
durch
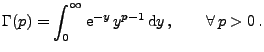
![]() spielen eine
wichtige Rolle bei der Zeitransformation von
Lévy-Prozessen.
spielen eine
wichtige Rolle bei der Zeitransformation von
Lévy-Prozessen.