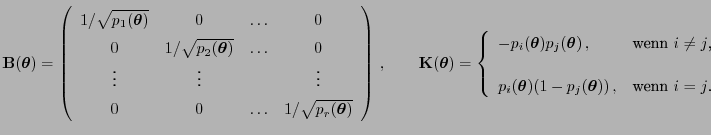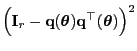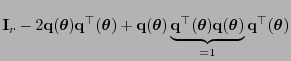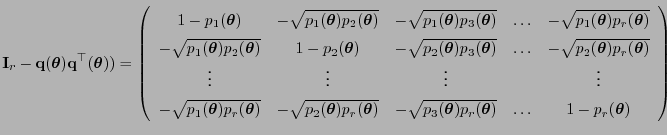Nächste Seite: Beispiele
Aufwärts: -Anpassungstest von Pearson-Fisher
Vorherige Seite: Fisher-Informationsmatrix und zentraler Grenzwertsatz
Inhalt
Asymptotische Verteilung der
Pearson-Fisher-Statistik
Das folgende Theorem ist die Grundlage des  -Anpassungstests von Pearson-Fisher. Dabei setzen wir voraus, dass
-Anpassungstests von Pearson-Fisher. Dabei setzen wir voraus, dass
- die in (61) betrachtete Likelihood-Funktion des
vergröberten Modells den Regularitätsbedingungen von
Abschnitt 5.3.2 genügt,
- die in (62) gegebene Fisher-Informationsmatrix
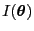 positiv definit ist und dass
positiv definit ist und dass
-
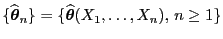 eine schwach konsistente Folge von ML-Schätzern für
eine schwach konsistente Folge von ML-Schätzern für
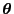 ist, die durch die Beobachtung des vergröberten
Modells gewonnen werden.
ist, die durch die Beobachtung des vergröberten
Modells gewonnen werden.
Ein mathematisch strikter Beweis von Theorem 5.9
kann durch Reinterpretation des  -Anpassungstests von
Pearson-Fisher als Likelihood-Quotiententest geführt
werden, vgl. beispielsweise Abschnitt 4.7 in H. Pruscha (2000)
Vorlesungen über mathematische Statistik, Teubner-Verlag,
Stuttgart.
-Anpassungstests von
Pearson-Fisher als Likelihood-Quotiententest geführt
werden, vgl. beispielsweise Abschnitt 4.7 in H. Pruscha (2000)
Vorlesungen über mathematische Statistik, Teubner-Verlag,
Stuttgart.
Weil diese Beweistechnik jedoch relativ komplex ist, geben wir
hier lediglich eine Herleitung von Theorem 5.9 an,
die teilweise heuristisch ist.
- Und zwar sei
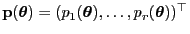 und
und
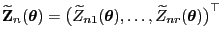 mit
mit
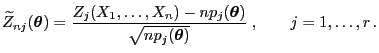 |
(71) |
- Weil
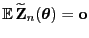 und weil sich
und weil sich
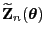 als Summe von
als Summe von  unabhängigen und
identisch verteilten Zufallsvektoren darstellen lässt, ergibt sich
aus dem multivariaten zentralen Grenzwertsatz (genauso wie im
Beweis von Theorem 5.5), dass
unabhängigen und
identisch verteilten Zufallsvektoren darstellen lässt, ergibt sich
aus dem multivariaten zentralen Grenzwertsatz (genauso wie im
Beweis von Theorem 5.5), dass
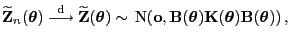 |
(72) |
wobei
- Für die Kovarianzmatrix
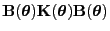 in
(72) gilt somit
in
(72) gilt somit
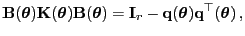 wobei wobei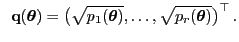 |
(73) |
- Für die in (63) eingeführte Matrix
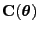 gilt wegen (68), dass
gilt wegen (68), dass
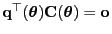 und somit
und somit
- Aus (72) und (73) ergibt sich nun,
dass
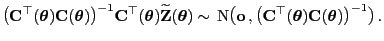 |
(74) |
- Außerdem ergibt sich aus Korollar 5.1 durch
Taylor-Reihenentwicklung, dass
- Hieraus und aus (74) folgt, dass
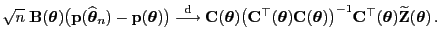 |
(75) |
- Andererseits ergibt sich aus (69) und
(71), dass
- wobei sich die letzte Gleichheit aus der Null-Konvergenz
ergibt, die aus
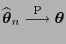 und dem
Continuous-Mapping-Theorem für Zufallsvektoren (vgl.
Lemma 4.5) folgt.
und dem
Continuous-Mapping-Theorem für Zufallsvektoren (vgl.
Lemma 4.5) folgt.
- Mit anderen Worten: Mit der Schreibweise
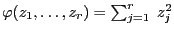 gilt
gilt
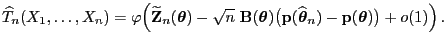 |
(76) |
- Zusammen mit (72) und (75)
suggeriert die asymptotische Näherungsformel (76)
die Vermutung, dass für
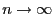
 |
(77) |
- Die Verteilungskonvergenz (77) ergibt sich jedoch
nicht direkt aus (72), (75)
und (76), sondern sie erfordert einen separaten Beweis, der hier weggelassen wird.
- Wir zeigen nun noch, dass
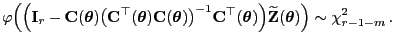 |
(78) |
- In (72) und (73) hatten wir
gezeigt, dass
- Außerdem ergibt sich aus
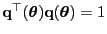 , dass
, dass
- d.h., die Kovarianzmatrix
des Zufallsvektors
 ist symmetrisch
und idempotent.
ist symmetrisch
und idempotent.
- Hieraus und aus der ersten Teilaussage von
Theorem 1.4 ergibt sich nun die Darstellungsformel
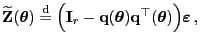 |
(79) |
wobei
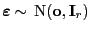 .
.
- Außerdem ist auch die Matrix
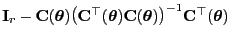 symmetrisch und
idempotent, und aus
symmetrisch und
idempotent, und aus
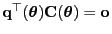 ergibt sich, dass
ergibt sich, dass
- Hieraus folgt, dass die Matrix
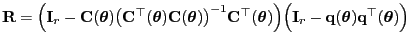 ebenfalls symmetrisch und idempotent ist.
ebenfalls symmetrisch und idempotent ist.
- Aus (79) und aus Theorem 1.9 ergibt
sich nun, dass
- Mit Hilfe von
Lemma 1.3 ergibt sich für den Rang
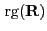 der
symmetrischen und idempotenten Matrix
der
symmetrischen und idempotenten Matrix
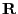 , dass
, dass
- Damit ist die Gültigkeit von (78) bewiesen.
- Beachte
 Bei der praktischen Durchführung des
Bei der praktischen Durchführung des  -Anpassungstests
von Pearson-Fisher kann ähnlich wie in
Abschnitt 5.2.2 vorgegangen werden, um die Hypothese
-Anpassungstests
von Pearson-Fisher kann ähnlich wie in
Abschnitt 5.2.2 vorgegangen werden, um die Hypothese
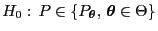 zu prüfen.
zu prüfen.




Nächste Seite: Beispiele
Aufwärts: -Anpassungstest von Pearson-Fisher
Vorherige Seite: Fisher-Informationsmatrix und zentraler Grenzwertsatz
Inhalt
Hendrik Schmidt
2006-02-27
![]() -Anpassungstests von Pearson-Fisher. Dabei setzen wir voraus, dass
-Anpassungstests von Pearson-Fisher. Dabei setzen wir voraus, dass
![]() -Anpassungstests von
Pearson-Fisher als Likelihood-Quotiententest geführt
werden, vgl. beispielsweise Abschnitt 4.7 in H. Pruscha (2000)
Vorlesungen über mathematische Statistik, Teubner-Verlag,
Stuttgart.
-Anpassungstests von
Pearson-Fisher als Likelihood-Quotiententest geführt
werden, vgl. beispielsweise Abschnitt 4.7 in H. Pruscha (2000)
Vorlesungen über mathematische Statistik, Teubner-Verlag,
Stuttgart.