Next: Specification of the Model
Up: skript_engl
Previous: Introduction
Contents
Markov Chains
- Markov chains can describe the (temporal) dynamics of objects,
systems, etc.
- that can possess one of finitely or countably many
possible configurations at a given time,
- where these configurations will be called the states of the
considered object or system, respectively.
- Examples for this class of objects and systems are
- the current prices of products like insurance policies, stocks or
bonds, if they are observed on a discrete (e.g. integer) time scale,
- the monthly profit of a business,
- the current length of the checkout lines (so-called ``queues'')
in a grocery store,
- the vector of temperature, air pressure, precipitation and wind
velocity recorded on an hourly basis at the meteorological office
Ulm-Kuhberg,
- digital maps, for example describing the momentary spatial
dispersion of a disease.
- microscopical 2D or 3D images describing the current state (i.e.
structural geometrical properties) of biological tissues or
technical materials such as metals or ceramics.
- Remarks
-
- In this course we will focus on discrete-time Markov
chains, i.e., the temporal dynamics of the considered objects,
systems etc. will be observed stepwise, e.g. at integer
points in time.
- The algorithms for Markov Chain Monte Carlo simulation we will
discuss in part II of the course are based on exactly these
discrete-time Markov chains.
- The number of potential states can be very high.
- For mathematical reasons it is therefore convenient to consider the
case of infinitely many states as well. As long as the infinite case
is restricted to countably many states, only slight
methodological changes will be necessary.
Subsections




Next: Specification of the Model
Up: skript_engl
Previous: Introduction
Contents
Ursa Pantle
2006-07-20
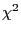 Contrast
Contrast
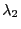 and
and