



Next: -Anpassungstest von Pearson
Up: skript
Previous: Dreifaktorielle Varianzanalyse
Contents
Tests von Verteilungsannahmen
- Die Zufallsstichprobe
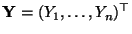 sei gegeben
durch das lineare Modell
sei gegeben
durch das lineare Modell
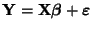 , wobei die
Designmatrix
, wobei die
Designmatrix
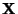 eine beliebige
eine beliebige 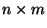 Matrix ist mit
Matrix ist mit
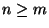 und vollem Spaltenrang
und vollem Spaltenrang
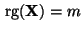 .
.
- So wie bisher sei
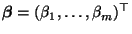 ein
(unbekannter) Parametervektor, und
ein
(unbekannter) Parametervektor, und
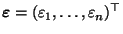 sei ein Vektor von zufälligen
Störgrößen
sei ein Vektor von zufälligen
Störgrößen
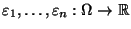 , die unabhängig und
identisch verteilt seien.
, die unabhängig und
identisch verteilt seien.
- In mehreren Abschnitten der Kapitel 2 -
4 hatten wir zusätzlich angenommen, daß die
Störgrößen
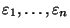 normalverteilt sind, d.h.,
normalverteilt sind, d.h.,
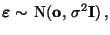 |
(1) |
wobei
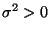 ein weiterer Modellparameter ist.
ein weiterer Modellparameter ist.
- Wenn wir unsicher sind, ob (1) gilt, dann können
wir diese zusätzliche Modellannahme wie folgt durch die
Beobachtung der Zufallsstichprobe
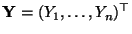 verifizieren.
verifizieren.
- Zur Erinnerung: Aus (1) und aus
Theorem 3.9 folgt, daß die Verteilung des Vektors
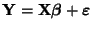 der Stichprobenvariablen bzw. des
MKQ-Schätzers
der Stichprobenvariablen bzw. des
MKQ-Schätzers
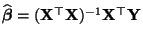 gegeben
ist durch
gegeben
ist durch
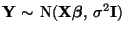
und
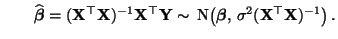
- Hieraus ergibt sich, daß
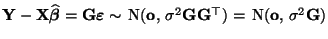 , weil die
, weil die 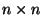 Matrix
Matrix
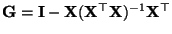 gemäß
Lemma 4.7 idempotent und symmetrisch ist mit
gemäß
Lemma 4.7 idempotent und symmetrisch ist mit
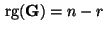 .
.
- Ähnlich wie im Beweis von Lemma 3.9 kann man zeigen,
daß
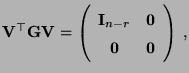 |
(2) |
wobei
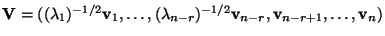 eine
eine 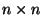 Matrix mit orthogonalen Spaltenvektoren ist, so
daß
Matrix mit orthogonalen Spaltenvektoren ist, so
daß
 orthonormale Eigenvektoren sind,
die zu den positiven Eigenwerten
orthonormale Eigenvektoren sind,
die zu den positiven Eigenwerten
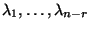 von
von
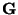 gehören, und
gehören, und
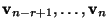 orthonormale Eigenvektoren sind, die zu dem Eigenwert 0 gehören.
orthonormale Eigenvektoren sind, die zu dem Eigenwert 0 gehören.
- Dann gilt
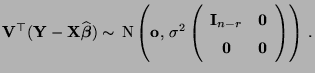 |
(3) |
- Mit anderen Worten: Aus (3) folgt, daß die ersten
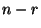 Komponenten des Vektors
Komponenten des Vektors
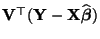 unabhängig und
N
unabhängig und
N
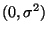 -verteilt sind.
-verteilt sind.
- Falls
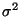 bekannt ist, dann können wir das Vorliegen der
N
bekannt ist, dann können wir das Vorliegen der
N
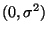 -Verteilung beispielsweise mit dem in
Abschnitt 5.1 diskutierten
-Verteilung beispielsweise mit dem in
Abschnitt 5.1 diskutierten 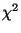 -Anpassungstests
verifizieren. Falls
-Anpassungstests
verifizieren. Falls 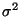 unbekannt ist, dann kann das
Vorliegen einer Normalverteilung mit einem modifizierten
unbekannt ist, dann kann das
Vorliegen einer Normalverteilung mit einem modifizierten
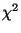 -Anpassungstest verifiziert werden, der in
Abschnitt 5.2 diskutiert wird.
-Anpassungstest verifiziert werden, der in
Abschnitt 5.2 diskutiert wird.
Subsections




Next: -Anpassungstest von Pearson
Up: skript
Previous: Dreifaktorielle Varianzanalyse
Contents
Ursa Pantle
2003-03-10