



Nächste Seite: Kolmogorow-Smirnow-Test
Aufwärts: skript
Vorherige Seite: Bewertung der Anpassungsgüte
Inhalt
Tests von Verteilungsannahmen
- In diesem Kapitel bezeichnen wir die Stichprobenvariablen mit
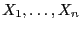 , wobei wir von jetzt an stets voraussetzen, dass
, wobei wir von jetzt an stets voraussetzen, dass
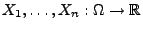 eine Folge von unabhängigen und identisch verteilten Zufallsvariablen ist.
eine Folge von unabhängigen und identisch verteilten Zufallsvariablen ist.
- Die Annahmen, die wir bisher über die Verteilung
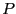 der
Stichprobenvariablen
der
Stichprobenvariablen
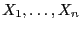 gemacht haben, waren
entweder rein qualitativ (diskrete bzw. absolutstetige
Verteilung) oder parametrisch, wobei in diesem Fall
vorausgesetzt wurde,
gemacht haben, waren
entweder rein qualitativ (diskrete bzw. absolutstetige
Verteilung) oder parametrisch, wobei in diesem Fall
vorausgesetzt wurde,
- dass
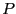 zu einer parametrischen Familie
zu einer parametrischen Familie
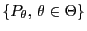 von Verteilungen mit
von Verteilungen mit
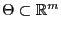 gehört
gehört
- und dass lediglich der Parametervektor
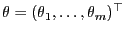 bzw. ein Teil seiner
Komponenten unbekannt ist.
bzw. ein Teil seiner
Komponenten unbekannt ist.
- Im Folgenden diskutieren wir nun so genannte Anpassungstests, die in der englischsprachigen Literatur Goodness-of-Fit-Tests genannt werden.
- Dabei betrachten wir zunächst einen Test, um die Hypothese
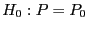 zu verifizieren, dass die Verteilung
zu verifizieren, dass die Verteilung 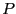 der
Stichprobenvariablen gleich einer vorgegebenen (hypothetischen)
Verteilung
der
Stichprobenvariablen gleich einer vorgegebenen (hypothetischen)
Verteilung 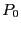 ist.
ist.
- Anschließend konstruieren wir Tests, um zu prüfen, ob
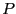 zu einer
vorgegebenen (parametrischen) Klasse von Verteilungen
zu einer
vorgegebenen (parametrischen) Klasse von Verteilungen
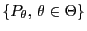 gehört.
gehört.
Unterabschnitte
Hendrik Schmidt
2006-02-27
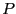 zu einer parametrischen Familie
zu einer parametrischen Familie
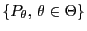 von Verteilungen mit
von Verteilungen mit
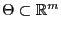 gehört
gehört
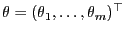 bzw. ein Teil seiner
Komponenten unbekannt ist.
bzw. ein Teil seiner
Komponenten unbekannt ist.
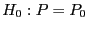 zu verifizieren, dass die Verteilung
zu verifizieren, dass die Verteilung 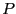 der
Stichprobenvariablen gleich einer vorgegebenen (hypothetischen)
Verteilung
der
Stichprobenvariablen gleich einer vorgegebenen (hypothetischen)
Verteilung 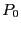 ist.
ist.
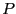 zu einer
vorgegebenen (parametrischen) Klasse von Verteilungen
zu einer
vorgegebenen (parametrischen) Klasse von Verteilungen
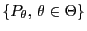 gehört.
gehört.